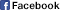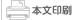半導体プロセスまるわかり　ロジック回路と同期/非同期

2014年01月27日 12時00分更新

　前回はトランジスタで構成されるデジタル回路について説明した。今回も引き続き、プロセスの基本的なことを解説していく。テーマはロジック回路、それと同期/非同期回路についてだ。

	ロジック回路実験基板

プロセッサー内部の基本となる
ブール代数とロジック回路

　デジタル回路、あるいはロジック回路と呼ぶこともあるが、これの基礎になっているのがブール代数という記号論理学である。最初にこれを発案したのは19世紀の数学者であるGeorge Booleで、彼の名をとってブール代数(Boolean Algebra)と呼ぶ。

　もっともブール代数そのものがロジック回路に出現するわけではなく、このブール代数をベースに考案された、組み合わせ回路と呼ばれるものが広く使われている。

　その一番基本的なものが、図1に示す3つである。NOTは唯一の1入力で、入ってきた信号をひっくり返すもの。入力Aが0なら1を、Aが1なら0をそれぞれ出力する。前回インバーターとして示した2つのMOSFETを組み合わせた回路が、このNOPとして動く。


図1　基本的なロジック回路

　他に、AとBの2つの入力の「どちらかが」1だったら1を返すOR(論理和)、それとAとBの「両方が」1だった時のみ1を返すANDがある。これを組み合わせることで、さらにNOR/NAND/XORといった回路(図2)も考えられる。


図2　NOR/NAND/XOR回路

　NORはOR＋NOTで「AとBが両方0の時だけ1」だし、NANDはAND＋NOTで「AとBが両方１の時だけ0」である。XORはORの拡張版で、「AとBの値が異なる時だけ1」といった働きをする。このNOR/NAND/XORあたりまでを「基本的なロジック回路」と分類することが多い。

　もっと厳密に言えば、NANDとNOR、NOTがあれば、残りの3種類のロジック回路をすべて作れるので、基本的という場合にはNANDとNOR、NOTの3つを指すこともある。

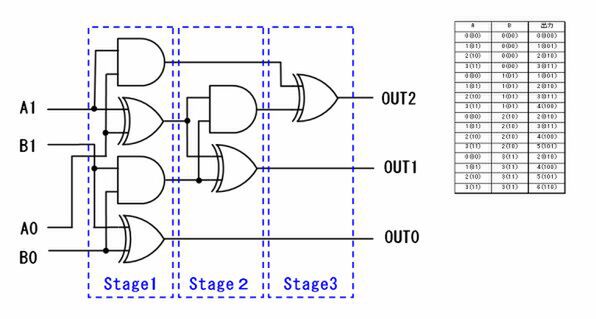
　さて、これを組み合わせるとなにができるかだが、実はプロセッサーの内部回路は全部この組み合わせだけでできている。つまり6種類だけで全部片付くわけだ。一例として、図3には2bitの加算器(Adder)の例を示した。


図3　2bitの加算器

　2bitの入力AとBは、どちらも0～3の値を取る。なので、組み合わせとしては0～6の範囲の結果が出ることになる。別にこの回路そのものを理解する必要はないのだが、簡単に説明すると以下のとおりになる。

Stage 1	A0とB0、A1とB1をそれぞれ加算する(XOR)とともに、桁上がりの計算も行なう(AND)
Stage 2	1桁目(A0とB0)の桁上がり分と、2桁目(A1とB2)の結果を加算するとともに、その桁上がりも計算する
Stage 3	2桁目の桁上がりを確定する

　この回路は説明用にわざと愚直な実装にしてあるので、実際はもう少しスマートな方法があるし、なによりこの方式では桁が増えるとどんどんStage数が増えてってしまってあまり実用的ではないのだが、それは説明用ということでご容赦いただきたい。

前へ 1 2 3 次へ