今回解説するBlaizeのGSPは、最近デンソーとの絡みで報道されることが多い。というのはデンソーが同社に少なからずの出資をしており、それもあって取締役会に人を出しているからということもある。
それに加えてデンソー子会社のNSI-TEXE(海外の会社に見えるが、品川に本社を置く日本の会社である)と技術協力しており、NSI-TEXEのDFP(Data Flow Processor)のコア技術はBlaize(というかThinCI)から供与を受けている部分が少なからずあること、あるいはそのNSI-TEXEがBlaize製品の日本で拡販を担当するといった形で意外に日本との関係が深いことが理由の1つ(それだけではないが)であろう。
そのBlaizeという会社、創業時はThinCI(シンクアイと発音する)という社名である。創業は2012年であるが、当初はStealthモード(外部に細かい情報を一切出さない状態)での運営となった。創業者はDinakar Munagala氏(CEO)とSatyaki Koneru氏(CTO)、Ke Yin氏(Chief Scientist and VP of Engineering)、それとVal G.Cock氏(Chief Software Architect)の4人である。
実はこの4人、前職が全員インテルの、それもチップセット関連である。もっと言えばチップセットの中でも特にGPU関係である。全員がGPUのアーキテクチャーやデザインの設計に携わってきたチームであり、時期的にはSandy Bridge世代あたりまでを担当。Ivy Bridge向けが一段落したあたりで離職してThinCIを創業した感じだ。
グラフ理論とは?
さてそのThinCIが開発していたのがGSP(Graph Streaming Processor)である。Stealthモードと言いつつThinCIは2017年のHotChipsで、同社のGSPについて説明したので、まずこの内容をご紹介したい。
グラフ理論は今まで連載の中でまともに説明してこなかったので、まずはこの話を。「巡回セールスマン問題」という言葉を聞いたことはおありだろうか? 過去記事を漁ってみると、例えばこれや、古い所ではこれなども引っかかる。
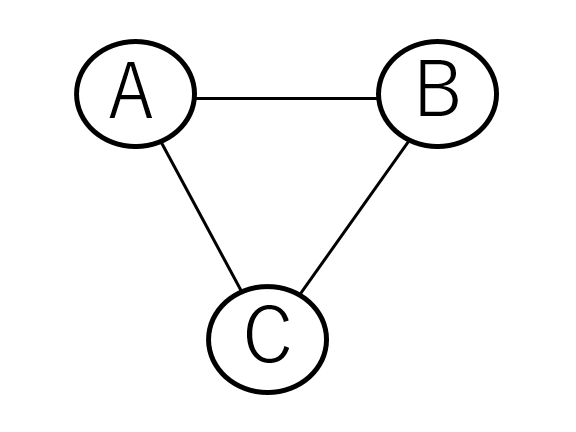
あるセールスマンが複数の都市をそれぞれ一度ずつ訪問し、最後に元の都市に戻るとしたとき最適な、つまり一番移動コストが少ないルートはどれか? という古典的な問題だ。これ、都市の数が少なければ簡単である。例えば3つで都市Aから出発するとすれば、A→B→C→Aか、A→C→B→Aしかない。
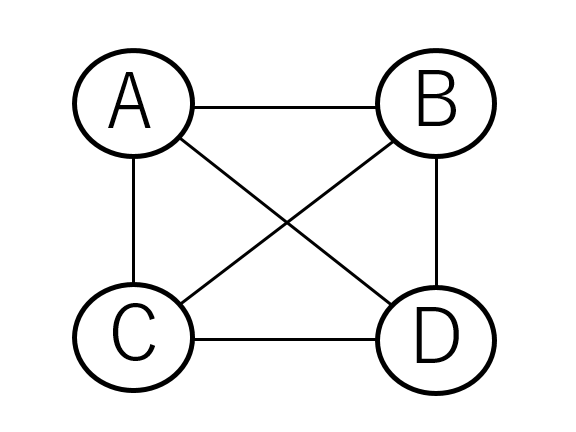
4つになるとやや複雑だが、Aから出発するとすれば以下の6通りだからまだ総当たりでなんとかなる。
A→B→C→D→A
A→B→D→C→A
A→C→B→D→A
A→C→D→B→A
A→D→B→C→A
A→D→C→B→A
ところが都市の数が増えていくと急速に計算量が増えていくことになる。計算機理論ではこの巡回セールスマン問題は「NP困難」に分類されている。NP(Non-deterministic Polynomial time)というのは多項式時間(ある多項式を解くために必要な時間)で計算できる(*1)という意味である。
(*1) 厳密には他にNPには要件があるが、計算機学科の授業ではないので割愛する。
ちなみにこの多項式時間、しばしばO(xxx)という表現で示される。Oというのはオーダーの意味で、例えばO(n)だったら、「要素がn個だと、計算時間がnにほぼ比例する」の意味である。世の中にはO(n2)やO(n3)、あるいはO(2n)という問題が山ほどあり、それもあって少ない問題だとすぐ計算できるが、ある程度以上nの数が増えるとお手上げ、ということが少なくない。
さて巡回セールスマン問題の場合、バカ正直に計算すると計算量がO(n!)となる。n!はnの階乗であり以下のようになる。
| 巡回セールスマン問題の解答 | ||||||
|---|---|---|---|---|---|---|
| n | n! | |||||
| 1 | 1 | |||||
| 2 | 2 | |||||
| 3 | 6 | |||||
| 4 | 24 | |||||
| 5 | 120 | |||||
| 6 | 720 | |||||
| 7 | 5040 | |||||
| 8 | 40320 | |||||
| 9 | 362880 | |||||
| 10 | 3628800 | |||||
ラフに言って、nが6を超えると一桁づつ計算量が増えていく格好だ。nの数が少ないときは多項式で近似できるが、ある程度増えると多項式で近似しきれない。このためNPが「困難」というわけだ。こうした計算量の爆発する処理を、いかにして現実のプロセッサーで取り扱うかというところでいろいろ工夫や細工が行なわれているわけで、量子コンピューターがこうした問題に最適というのもゆえなき話ではない。
巡回セールスマン問題は極端な例であるが、このようにノード(節:図で言えばA~D)と、エッジ(A~Dをつなぐ直線)で構成されるものを数学では「グラフ」として扱っている。ニューラルネットワークもその意味ではやはりグラフである。
そもそも人間の脳がシナプスとニューロンで構成されており、シナプスがノード、ニューロンをエッジととらえればグラフの構造になっているわけだ。したがってグラフを上手くあつかえると、ニューラルネットワークの処理に役に立つことになる。

この連載の記事
-
第863回
PC
銅配線はなぜ限界なのか? ルテニウムへの移行で変わる半導体製造の常識と課題 -
第862回
PC
「ビル100階建て相当」の超難工事! DRAM微細化が限界を超え前人未到の垂直化へ突入 -
第861回
PC
INT4量子化+高度な電圧管理で消費電力60%削減かつ90%性能アップ! Snapdragon X2 Eliteの最先端技術を解説 -
第860回
PC
NVIDIAのVeraとRubinはPCIe Gen6対応、176スレッドの新アーキテクチャー搭載! 最高クラスの性能でAI開発を革新 -
第859回
デジタル
組み込み向けのAMD Ryzen AI Embedded P100シリーズはZen 5を最大6コア搭載で、最大50TOPSのNPU性能を実現 -
第858回
デジタル
CES 2026で実機を披露! AMDが発表した最先端AIラックHeliosの最新仕様を独自解説 -
第857回
PC
FinFETを超えるGAA構造の威力! Samsung推進のMBCFETが実現する高性能チップの未来 -
第856回
PC
Rubin Ultra搭載Kyber Rackが放つ100PFlops級ハイスペック性能と3600GB/s超NVLink接続の秘密を解析 -
第855回
PC
配線太さがジュース缶並み!? 800V DC供給で電力損失7~10%削減を可能にする次世代データセンターラック技術 -
第854回
PC
巨大ラジエーターで熱管理! NVIDIA GB200/300搭載NVL72ラックがもたらす次世代AIインフラの全貌 -
第853回
PC
7つのカメラと高度な6DOF・Depthセンサー搭載、Meta Orionが切り開く没入感抜群の新ARスマートグラス技術 - この連載の一覧へ