遠藤諭のプログラミング＋日記 第71回

映画『エッシャー視覚の魔術師』はファンなら必見の映画

渋谷道玄坂のマンホールの蓋のヒミツはご存じか？

外国人インスタグラマー（？）に渋谷のマンホールの蓋の秘密を教えてあげる。

　12月14日から映画『エッシャー視覚の魔術師』（2018年・イタリア）の公開がはじまった。エッシャーについては「M・C・エッシャーとでんぐりでんぐりの話」に少し踏み込んで書かせてもらったが、そのあたりの縁もあって公開日にトークをさせてもらった。

　日本テセレーションデザイン協会の会長で数学者の荒木義明さんにお声がけいただいて、アップリンク渋谷での公開日の上映後、対談をさせていただいた。ちなみに、この対談シリーズは４回予定されていて、12月22日（日）には、東京2020エンブレムをデザインされた野老朝雄さんである。

　映画は、エッシャーファンは絶対に観たほうがよいとても満足感の高いものになっている。作品とソックリのアングルでイタリアやスペインの実際の美しい風景が映し出される（エッシャーと同じ体験ができる！）。時間軸に沿って、日記や家族の証言や時代背景をもとに編集されることが、エッシャーについてはとても重要なのだった。

　1989年ベルエポックの時代に生まれて、２つの大戦をさはんで、1972年という人類が精神的なある決着点にいたる時代まで生きた。なんとなく、エッチングという版画手法が醸し出す超時代性や紋章や寓意画のような作品世界から、その背景がまるで想像できなくなっていたのだ。

配給バンドラ、2月頃にかけて日本各地で公開予定。ロビン・ルッツ監督、共同脚本のマラインケ・デ・ヨンケ氏へのインタビュー、錯視で有名な杉原厚吉東京大学名誉教授・明治大学研究特別教授の寄稿などを収録した公式パンフレットもうれしい。

　ということで、映画も楽しく見させてもらったうえに、とくにエッシャーの数学的だったりアルゴリズム的だったりするところを、それぞれ話させてもらった。

　ちなみに、テセレーション（tessellation：同じ図形で平面を埋め尽くす）は、エッシャー作品の代表的なモチーフである。私が最初にふれたエッシャー作品もこの“敷き詰め”ものだった。実際に、自分で読んだものはもっと後のものだが、1961年の『Scientific American』にマーチン・ガードナーという私の憧れの著者が、エッシャーを紹介していたのも、この数学的モザイクだった。

『Scientific American』誌の1961年4月号でのM・C・エッシャーの作品紹介

　このテセレーションには、私はいまのところ手を出していないのだが、なにしろもとがタイルの敷き詰めだから子供にもできる楽しさがある。実際に、日本テセレーションデザイン協会では、数学とアートの力を育むという「T3パズル」を使って、子どもたちにワークショップを行ったりしている（詳しくは公式サイトご覧あれ）。

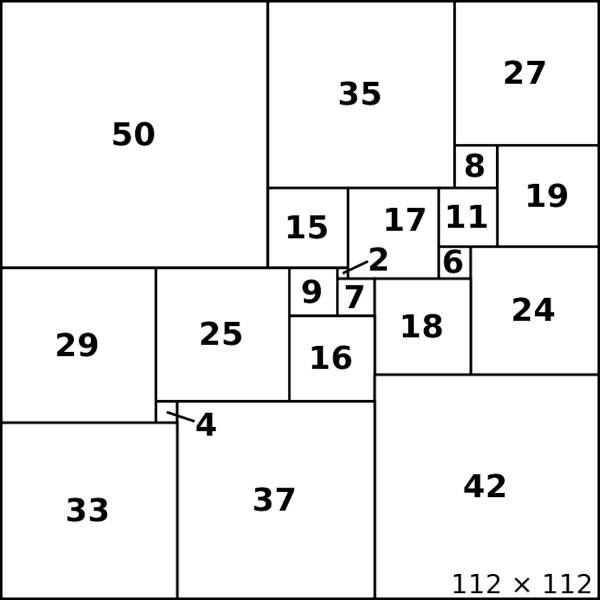
　個人的にいちばん好きな“敷き詰め”に関する問題は、１つの正方形をそれぞれ大きさの異なる正方形に分割できるかという「ニコライ・ルジン (Nikolai Luzin) の問題」である。そのような正方形のことを「正方分割正方形」などと呼んでいて、むかし『数学セミナー』誌かなにかで見つけて、それが電気回路の計算と置き換え可能であるというあたりを知ってめちゃちくゃ魅せられてしまった。

正方形を異なる大きさの正方形で分割する最小分割の解は21個。

　もしも、私が、よき時代の貴族かなにかだったら「ニコライ・ルジンの館」なんてのを作っただろう。建物全体が正方形なのに、それを割って作られた部屋がすべて正方形。しかも、１つとして同じ広さの部屋はない。部屋はそれぞれ違った色に壁が塗られている。入り口のドアには、最小の部屋「２」から順に部屋の大きさを示す整数値の名前がついている。

　さて、私の正方分割正方形に対する愛に比べると、テセレーションは応用性がきわめて高い。『エッシャー視覚の魔術師』のトークで、荒木義明氏は、最後にまさに映画が上映されている渋谷のハチ公で有名な道玄坂のマンホールの蓋がテセレーションであると紹介してくれた。

　以下が、実際に、上映とトークのあと道玄坂まで行って百軒店のあたりで見つけたマンホールの蓋。

一見ただのマンホールの蓋に見えるがよく見ると「人」の姿が並んでいることが分かる。

　ふだんこの道を頻繁に歩いている人もなんとなく模様が刻印されているんだろうなというくらいしか気づいていないらしい。しかし、よく見ると「人」がならんでなんだか走っているような感じに見える。そして、さらによく見ると真ん中に「DOG・EN・SAKA」と書かれた真鍮のプレートがはまっていて、「ドッグ？」となる。

横から見るとなんと「犬」が並んでいることがわかる！

　これはやっぱり、道玄坂なので「忠犬ハチ公」ということなのでしょうか？　「DOG・EN・SAKA」は「犬に縁のある坂」の意味になりますかね。

　実は、この犬くんの中にはそれぞれ１匹ずつシッポが巻いたものと首輪をしたものがいると「駅からマンホール」という楽しいサイトに書かれていると、これまた荒木さんに教えていただいた。さらには、同じページには、このマンホールをデザインされた岡康正さんのコメントまで入っているので、ぜひご覧あれ。なんとあのマンホールはリバーシブルで裏側は別なデザインにもなっているのだとか。

　我々は、百軒店のあたりからスクランブル交差点のあたりまで探して歩いたのだが、歩道の真ん中にあったり道路側やお店のひさしの下にあったり。たぶん、映画とトークをご覧になった方々も、我々と同じように道玄坂の歩道を観察しながら帰られた人が何人もおられたのではないかと思う。

マンホールの蓋を探す私と荒木義明氏。

　最後にちょっとだけ、映画とトークの話に戻させてもらうと、私は、昨年上野の森美術館などで開催された「ミラクルエッシャー展」の公式サイトにメッセージを寄せさせてもらった。荒木氏は、そこで私が書いた、

　「実は、子どもにもわかる平面タイル張り（敷き詰め）や不可能図形をずっと先までいくと本当の宇宙の秘密が隠されているんじゃないかとも思えます」

　というセリフをひろいあげてくれてトークのためのパワポに入れてくれた。宇宙に関する理論は、時代とともに大きく変化してきているのはご存じのとおり。エッシャーとも交流のあったロジャー・ペンローズは、ブラックホールの特異点定理、量子重力理論など、まさにこのあたりで超むずかしい研究をしている。しかし、ペンローズは、敷き詰め問題（ペンローズタイル）や不可能図形でも有名なのだった。

　エッシャーの《滝》や《上昇と下降》などの作品は、ペンローズと彼の父親であるライオネル・ペンローズの考えた不可能図形にヒントを得ている。ひょっとしたら、父親のライオネルが遺伝学者であったことも無関係ではないような気もしてくる。

　宇宙、生命、数学、アルゴリズムなどと、往年のテレビドラマ『ベン・ケーシー』（誰も分からないか？）のオープニングのように読み上げながら、マンホールの蓋さがしのあとあらためて妄想していた私だった。

道玄坂と文化村通りに分かれるところにある109が見えるところにもある。

---

【参考リンク】
『エッシャー視覚の魔術師』http://pan-dora.co.jp/escher/
日本テセレーションデザイン協会 https://www.tessellation.jp/
アップリンク https://www.uplink.co.jp/

遠藤諭（えんどうさとし）

　株式会社角川アスキー総合研究所 主席研究員。月刊アスキー編集長などを経て、2013年より現職。雑誌編集のかたわらミリオンセラーとなった『マーフィーの法則』など書籍の企画も手掛ける。角川アスキー総研では、スマートフォンとネットの時代の人々のライフスタイルに関して、調査・コンサルティングを行っている。著書に、『近代プログラマの夕』（ホーテンス・S・エンドウ名義、アスキー）、『計算機屋かく戦えり』など。

Twitter：@hortense667
Facebook：https://www.facebook.com/satoshi.endo.773