ロードマップでわかる！当世プロセッサー事情 第468回

いまさら聞けないIT用語集　浮動小数点演算の単精度と倍精度って？

基本となる単精度浮動小数点演算
2進数を10進数に変換すると誤差が生まれる

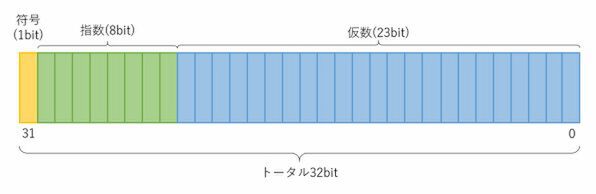
　まず基本であるBinary32の説明をしよう。いわゆる単精度浮動小数点演算と呼ばれているものに使われるのがこれだ。この内部フォーマットは下図のようになっている。

単精度浮動小数点演算の内部フォーマット

　「あれ、上の表と仮数のサイズが違う」といわれそうだが、上の表は仮数部に符号bitを含んだものになっている。つまり符号+23bitで合計24bitという表現である。

　さて、符号bitは0なら正、1なら負でこれはダイレクトだが、その先はやや複雑な仕組みである。まず指数部。00000000(0)の場合は数字そのものが0、もしくは非正規数(0ではないけど、限りなく0に近い小さな数字)を、11111111(255)の場合は無限大もしくはNaN(Not a Number：数字ではない)を意味する。

　普通の数字なら00000001(1)～11111110(254)までの範囲になるのだが、ここから127を引いて-126～127の値を表現する。つまり2^-126～2¹²⁷という範囲になる。

　一方仮数部。こちらは指数部が0でない場合、最上位に暗黙の“1”を立てる。すると仮数部は23bit分しかないにもかかわらず、実質的に24bit分になる。

　これが大きいのは、23bitでは10進相当で6.923桁分で、つまり有効数字が7桁にならない。ところが24bitにすると7.224桁分で、有効数字が7桁になるためである。よって仮数部の表現は頭に1がついており、これが"1."に相当する。下の例がわかりやすいだろう。

Binary32での演算
仮数部の表現	内部での扱い方	値
00000000000000000000000 10000000000000000000000 11000000000000000000000 11100000000000000000000 　　　　　　： 11111111111111111111111	100000000000000000000000 110000000000000000000000 111000000000000000000000 111100000000000000000000 　　　　　　： 111111111111111111111111	1.0 1.5 1.75 1.875 　： 1.99999988079071

　この「値」は2進数なので、1.0～1.999999...の範囲に収まる形になる。もちろんこれは内部表現であって、実際には10進数に内部で変換して出力することになる。

　Binary64/128/256は、単純に仮数部と指数部の桁が増える(結果、仮数部の有効数字が増え、また扱える値の範囲が広がる)し、逆にBinary16は桁が半分以下に落ちるので、有効数字・扱える値の範囲ともに狭まることになる。

　ちなみにDecimal32/64/128は、きちんと10進数の演算が必要な場合に利用される。Decimal32では以下のようになり、きちんと割り切れる数字ではない。

Decimal32での演算
仮数部の表現	内部での扱い方
00000000000000000000000 01000000000000000000000 00100000000000000000000 00010000000000000000000 00001000000000000000000 00000100000000000000000 00000010000000000000000 00000001000000000000000 00000000100000000000000 00000000010000000000000 00000000001000000000000 00000000000100000000000 00000000000010000000000 00000000000001000000000 00000000000000100000000 00000000000000010000000 00000000000000001000000 00000000000000000100000 00000000000000000010000 00000000000000000001000 00000000000000000000100 00000000000000000000010 00000000000000000000001	1.5 1.25 1.125 1.0625 1.03125 1.015625 1.0078125 1.00390625 1.001953125 1.0009765625 1.00048828125 1.000244140625 1.0001220703125 1.00006103515625 1.000030517578125 1.0000152587890625 1.00000762939453125 1.000003814697265125 1.0000019073486325625 1.00000095367431628125 1.000000476837153140625 1.0000002384185765703125 1.00000011920928828516625

　10進法なら1.1+0.1＝1.2は当たり前だが、2進法ではこれが「1.1に限りなく近い値」+「0.1に限りなく近い値」という計算になるため、たまに1.2にならない場合がありえる(有効数字次第ではあるが)。

　実はこれにまつわる有名な話がある。米軍のパトリオット地対空ミサイルが、湾岸戦争のさなかの1991年2月、イラク軍のスカッドミサイルの迎撃に失敗するという事件があった。

　この原因は、パトリオットの制御に利用していたプログラムが、内部で24bitのカウンターを利用して時間を測定していたのだが、2進/10進の変換の誤差が蓄積した結果、タイミングが0.34秒ずれたことである。

　原因がわかったことで、現場での対処(煩雑にシステムを再起動して誤差の蓄積を解消)が可能になったが、根本的には2進数をベースにするとどうしても誤差を避けられないということで、こうした用途向けに10進数ベースの浮動小数点フォーマットも追加されることになった。