本記事はTim SeverienとSimon Codringtonが査読を担当しています。最高のコンテンツに仕上げるために尽力してくれたSitePointの査読担当者のみなさんに感謝します。
「VR元年」とも言われる2016年、JavaScriptエンジニアは3Dプログラミングを学んだほうがいいかもしれません。
Webページで画像やフラットな図形を表示するのはとても簡単です。しかし、3D表現となると2Dよりも複雑なので少し難しくなります。3Dで表示するには、WebGLやThree.jsのような専用の技術やライブラリを使います。
ただし、立方体のような基本的な形を表示したいだけであれば、こうした技術を使う必要はありません。もっと言えば、これらの技術を使って表示できたとしても、どのようにして平面の画面に3D図形が表示されたのか理解するのは難しいでしょう。
この記事では、WebGLを使わずに簡単な3Dエンジンを作成する方法を説明します。最初に3D図形の格納方法について説明した後、2種類の投影法による表示方法を紹介します。
3D図形の格納と変換
すべての形は多面体である
仮想世界が現実世界と大きく異なる点は、連続性がなく、すべてが離散していることです。例えば、画面に完全な円を描くことはできませんが、たくさんエッジを効かせて正多角形を描いて円に近いものを表示することはできます。エッジが多くなればなるほど、より完璧な円に見えます。
3Dも同じことで、図形は3D画像の要素となる多角形(ポリゴン)で表せます。多面体(平面のみで、球のような曲線がない3次元図形)は多角形でできています。 立方体のような、すでに多面体である図形では驚くことではありませんが、球のような図形を表現する場合には覚えておくと役に立ちます。
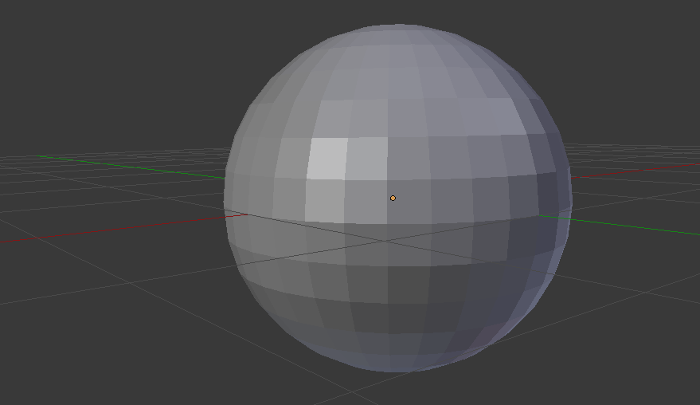
多面体を格納する
多面体の格納方法を考えるには、多面体のような形を数学ではどのように表すかを思い出す必要があります。学生時代にいくつか基本的な形状については学習しているはずです。例えば正方形なら、四隅の頂点をA 、B、C、Dとし、正方形ABCDと呼びます。
3Dエンジンでも同様です。図形の各頂点の座標を格納することから始めましょう。図形の表面をリストし、さらに各表面は表面を作る頂点座標をリストします。
頂点を表すには正しい構造が必要です。ここで、頂点の座標を格納するクラスを作ります。
var Vertex = function(x, y, z) {
this.x = parseFloat(x);
this.y = parseFloat(y);
this.z = parseFloat(z);
};
頂点が他のオブジェクトのように作成できました。
var A = new Vertex(10, 20, 0.5);
次に、多面体を表すクラスを作ります。立方体で作成してみましょう。クラスの定義は次の通りです。説明は後でします。
var Cube = function(center, size) {
// Generate the vertices
var d = size / 2;
this.vertices = [
new Vertex(center.x - d, center.y - d, center.z + d),
new Vertex(center.x - d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z - d),
new Vertex(center.x + d, center.y - d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z + d),
new Vertex(center.x + d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z - d),
new Vertex(center.x - d, center.y + d, center.z + d)
];
// Generate the faces
this.faces = [
[this.vertices[0], this.vertices[1], this.vertices[2], this.vertices[3]],
[this.vertices[3], this.vertices[2], this.vertices[5], this.vertices[4]],
[this.vertices[4], this.vertices[5], this.vertices[6], this.vertices[7]],
[this.vertices[7], this.vertices[6], this.vertices[1], this.vertices[0]],
[this.vertices[7], this.vertices[0], this.vertices[3], this.vertices[4]],
[this.vertices[1], this.vertices[6], this.vertices[5], this.vertices[2]]
];
};
このクラスを使うと、立方体の中心と側端の長さを指定すると仮想の立方体を作成できます。
var cube = new Cube(new Vertex(0, 0, 0), 200);
「Cube」クラスの作成は、立方体の頂点を作ることから始まります。頂点の位置は指定された中心の位置から算出されます。図の方がわかりやすいと思います。作成した8つの頂点の位置を見てください。
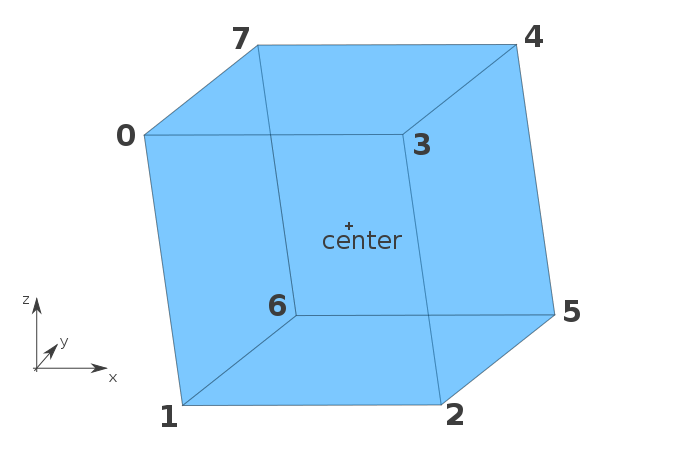
次に、表面をリストします。各表面は正方形なので、各表面に4つの頂点を指定します。ここでは配列で表面を表しましたが、必要ならば特定のクラスも作れます。
表面の作成には4つの頂点を使いますが、頂点の位置はthis.vertices[i]オブジェクトで保存されるので、再度指定する必要はありません。この方法をとったのは、実用的であることに加え、もう1つ理由があります。
JavaScriptは初期設定によって最小限のメモリを使うようになっています。メモリ使用量を抑えるために、関数の変数オブジェクトや、配列に保存されたオブジェクトでさえコピーしません。今回の方法にはぴったりです。
実際に、各頂点には3つの数字(頂点の座標)があり、さらに加えたいときのためにいくつかメソッドがあります。各表面の頂点のコピーを保存するには多くのメモリが必要ですが、まったく役に立ちません。役立つのは変数を参照するリファレンスです。座標(とその他のメソッド)は1回しか保存されません。各頂点は異なる3つの表面に使われるので、コピーではなくリファレンスを格納することで、必要なメモリはおおよそ3分の1になります!
三角形は必要?
もし、BlenderのようなソフトウェアやWebGLのようなライブラリーで3Dの経験があれば、三角形を使うほうがよいと聞いたことがあるかもしれませんね。ですが、あえて三角形は使っていません。
三角形を使わない理由は、本記事はJavaScriptを使った3Dエンジンの作成方法の紹介であり、立方体のような基本形を表示しようとしているからです。正方形を表示するのに三角形を使うと、今回の方法では他のものよりも複雑になってしまいます。
ただ、今後もっと完全なレンダラーを作るつもりなら、一般的には三角形が使われることを知っておくとよいでしょう。これには2つの理由があります。
- 1.テクスチャ
- 表面に画像を表示するには、数学的な理由から三角形が必要です。
- 2.変わった表面
- 3つの頂点はいつも同じ平面にありますが、4番目の頂点を違う平面に加えられます。そしてこの4つの頂点を結ぶ表面を作れます。このような場合、描く方法の選択肢はなく、表面を2つの三角形に分けなければなりません(1枚の紙を使ってやってみてください)。三角形を使うことで、どこで分割するのかを選ぶことができます(Tim、助言ありがとう!)。
多面体を動かす
コピーの代わりにリファレンスを格納することには、もう1つメリットがあります。多面体を修正したいときに、このシステムなら必要な操作も3分の1になるのです。理由を理解するために、数学の授業をもう一度思い出してみましょう。正方形を平行移動させたいとき、当然、本当に移動させるわけではありませんね。実際には、4つの頂点を平行移動してから結びます。
ここでも同じです。面を触るわけではありません。各頂点に必要な操作を適用して実行します。面はリファレンスを利用するので、面の座標は自動的に更新されます。先ほど作成した立方体を例に、どうやって平行移動させることができるか見てみましょう。
for (var i = 0; i < 8; ++i) {
cube.vertices[i].x += 50;
cube.vertices[i].y += 20;
cube.vertices[i].z += 15;
}
画像をレンダリングする
3Dオブジェクトの格納方法と、3Dオブジェクトの動かし方についてわかったところで、いよいよ表示方法に進みましょう。その前に、これからのことが分かりやすくなるように、理論の背景を少し説明しておきましょう。
投影
先ほど3D座標を格納しました。しかし、画面では2D座標しか表示できないので、3D座標を2D座標に変換する方法が必要になります。これは数学でいう「投影」です。3Dの2Dへの投影は、バーチャルカメラと呼ばれる新しいオブジェクトの抽象的な操作です。このカメラが3Dの物品を撮影し、その座標を2D座標に変換して画面に表示するレンダラーに送ります。このとき、カメラは3D空間の原点に置かれていると仮定します(座標は(0,0,0))。
本記事では冒頭から座標をx、y、zとして説明していますが、座標を定義するには、基底が必要です。zは頂点の座標ですか? zは上にありますか? 下にありますか? 絶対的な答えはなく、決まった方法もありません。実際は好きなように選べます。唯一気をつけなけれなならないのは、3Dオブジェクトを作るときはつじつまがあっていることです。そうしないと式が変わってしまいます。この記事では、基底は上記の立方体の図解の通り、xは左から右に、yは後ろから前に、zは下から上としました。
さて、何をするかおわかりですね。(x,y,z)基底の座標を表示するためには、(x,z)基底の座標に変換する必要があります。(x,z)基底なら平面なので、座標を表示できます。
投影法は1つだけではありません。なんと、投影法は無数にあります! では実践でもっとも役に立つ、2つの投影法についてみてみましょう。
シーンをレンダーする方法
図形を投影する前に、オブジェクトを表示する関数を書きましょう。この関数は、レンダーするためにオブジェクトをリストしている配列、オブジェクト表示に欠かせないキャンバスのコンテキスト、正しい位置にオブジェクトを描くのに必要なその他の詳細情報をパラメータとして受け取ります。
配列にはレンダーするオブジェクトをいくつか含めることができますが、1つ守らなければならないことがあります。facesというパブリックプロパティを作ることです。facesは(先ほど作成した立方体のような)オブジェクトのすべての表面をリストしている配列です。これらの表面は(正方形、三角形、十二角形でさえ)どんな形にもなります。頂点をリストしている配列になることが求められるだけなのです。
関数のコードを見てみましょう。この後、説明をします。
function render(objects, ctx, dx, dy) {
// For each object
for (var i = 0, n_obj = objects.length; i < n_obj; ++i) {
// For each face
for (var j = 0, n_faces = objects[i].faces.length; j < n_faces; ++j) {
// Current face
var face = objects[i].faces[j];
// Draw the first vertex
var P = project(face[0]);
ctx.beginPath();
ctx.moveTo(P.x + dx, -P.y + dy);
// Draw the other vertices
for (var k = 1, n_vertices = face.length; k < n_vertices; ++k) {
P = project(face[k]);
ctx.lineTo(P.x + dx, -P.y + dy);
}
// Close the path and draw the face
ctx.closePath();
ctx.stroke();
ctx.fill();
}
}
}
この関数についてはもう少し説明が必要でしょう。project()関数とは何か、またdx、dyの値とは何か、より明確にしなくてはなりません。あとは、基本的にオブジェクトのリストと各表面の描き方だけです。
project()関数はその名からも分かるように、3D座標を2D座標に変換します。以下のように定義して、3D空間で頂点を受け取り、2D平面の頂点に返します。
var Vertex2D = function(x, y) {
this.x = parseFloat(x);
this.y = parseFloat(y);
};
xとz座標を指定する代わりに、z座標をyに付け替えました。2D形状ではよく見かけるやり方ですが、zを使い続けることもできます。
project()の具体的な内容は、投影法の種類によって変わるので、次のセクションで説明しましょう。どの投影法を選んでもrender()関数は今のまま使えます。
平面に座標を設定すれば、キャンバス上に表示できます。まさに表示しようとしているのですが…、ちょっとしたトリックが必要です。project()関数で返された実際の座標を本当に描くわけではありませんよ。
実際に、project()関数は仮想の2D平面の座標を返しますが、原点は3D空間で定義されたのと同じです。ここでは原点をキャンバスの中心にしたいので座標を平行移動させます。頂点(0,0)はキャンバスの中心ではありませんが、dxとdyを賢く使って(0 + dx,0 + dy)とすれば中心になります。(dx,dy)をキャンバスの中心にする方法は絞られていて、dx = canvas.width / 2、dy = canvas.height / 2と定義します。
最後に詳細です。なぜ直接yを使わず-yを使うのでしょうか? 答えは基底の選択にあります。z軸は上に向かっています。元の3D空間では、正のz座標にある頂点は上に移動します。しかしキャンバスではy軸は下に向かっていて、正のy座標にある頂点は下に移動します。ですから、キャンバス上のy座標は、元の3D空間のz座標とは反対に定義する必要があるのです。
render()関数について分かったところで、project()関数に進みましょう。
正投影図
正投影図の説明から始めましょう。一番簡単なので、完全に理解できるはずです。
3つの座標があって、これを2つだけにしたい。このような場合、どのようにするのが一番簡単ですか? 座標の1つを削ることですね。これが正投影図の原理です。奥行を示すy座標を削るのです。
function project(M) {
return new Vertex2D(M.x, M.z);
}
さあ、書いてきたコードで試してみましょう。うまくいきましたね! おめでとうございます、平面のスクリーン上に3Dオブジェクトが表示されました!
この関数は次の実例で実行されています。マウスで立方体を回転させて操作できます。
正投影図は平行がきちんと表現できるので好まれるますが、一番自然な見え方ではありません。人の目は正投影図のようには見ないからです。それでは、2番目の投影法である透視図を紹介しましょう。
透視図
透視図は正投影図に比べて計算が必要になる分、多少複雑ですが、それほど難しい計算ではありません。ただし、切片定理(intercept theorem)を使います。
なぜ正投影図が自然に見えないかを理解するために、図で確かめましょう。点線は平面に対して直角に投影しています。
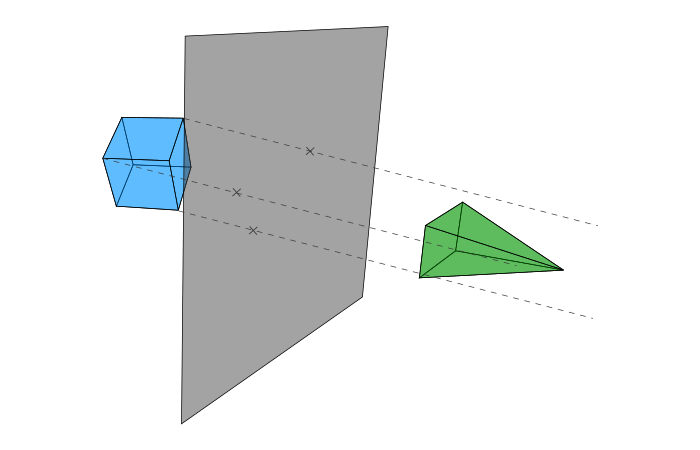
しかし現実には、次の図に近いように見ます。
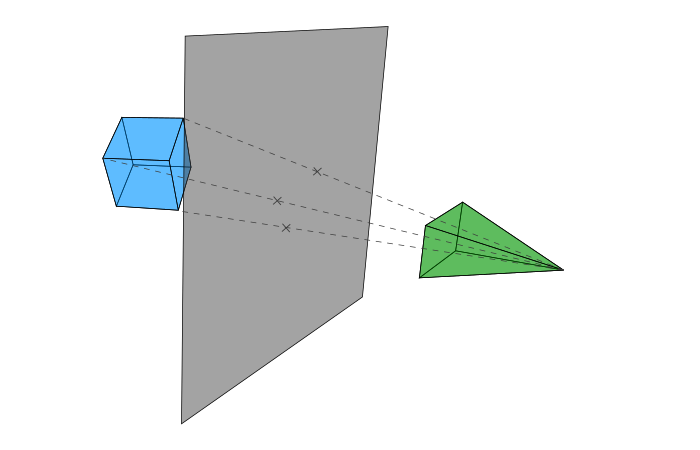
基本的に次の2段階あります。
- 原図の頂点とカメラの原点を結ぶ
- この結んだ線と平面の交差が投影
正投影図に対して、透視図では平面の正確な位置が重要です。平面をカメラから離れた位置に置くと、近くに置いたときと同じような効果は得られません。ここでは、カメラからの距離をdとします。
3D空間の頂点 M(x,y,z)から、平面上の投影図M'の座標(x',z')を計算します。
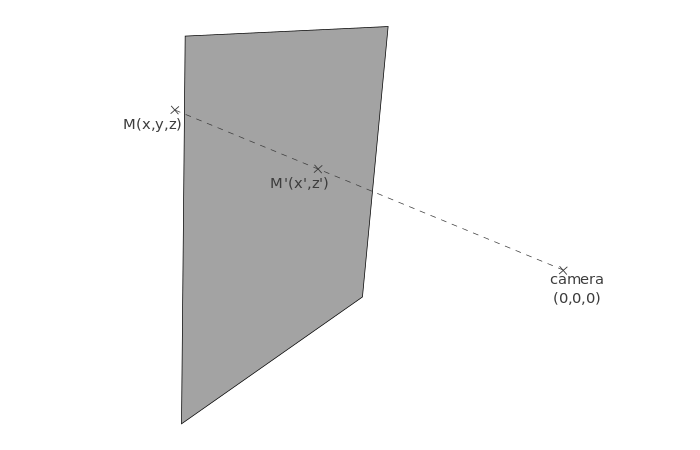
どうやってこれらの座標を算出するか見当がつくように、違う視点に立って、図を上から見てみましょう。
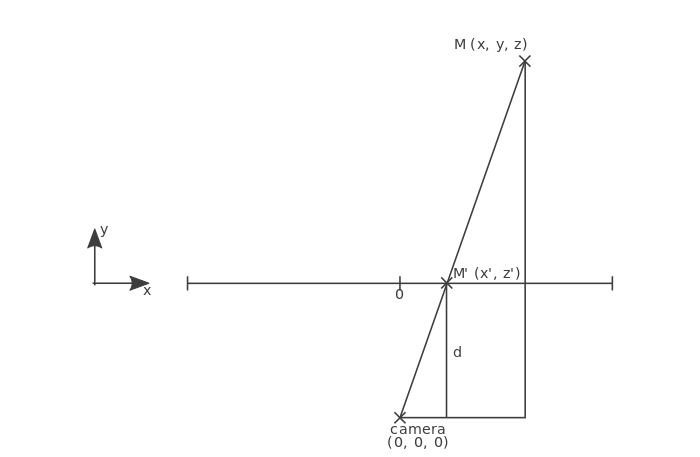
切片定理で使われる配置であることがわかりますね。上の図では、他との位置関係からx、 y、 dの値がわかります。 x'を計算したいので、切片定理を適用し、x' = d / y * xの方程式を立てます。
次に、横から同じ図をみると、似たような図が見えます。z、 yとd: z' = d / y * zの計算からz'の値を求めることができます。
もう透視図のproject()関数を書くことができますね。
function project(M) {
// Distance between the camera and the plane
var d = 200;
var r = d / M.y;
return new Vertex2D(r * M.x, r * M.z);
}
この関数は次の例で試せます。もう一度、立方体を動かし操作してみてください。
最後に
作成した超基本的な3Dエンジンは、どんな3D図形も表示できるようになりました。うまく表示できるようになるためのポイントがいくつかあります。ポイントの1つは、裏側を含め、図形の各表面を見ることです。裏側を非表示にするには、back-face cullingを使います。
今回はテクスチャについては説明しなかったので、すべての図形が同じ色になっています。オブジェクトにcolorプロパティを追加すると、どのように描いたか分かるように色を変更できます。あまり変更せずに、1つの表面に1色の選択もできます。また、表面上に画像の表示もできます。ですが、もっと難しくなるので、説明には別の記事が必要でしょう。
他にも変更できます。空間の原点にカメラを置きましたが、動かせます(頂点を投影する前に基底を変更します)。カメラの裏側にある頂点が描かれていますが、隠したい場合はclipping planeで修正できます(分かりやすいですが、実行は少し難しいです)。
これまで説明してきたように、作成した3Dエンジンは完全には程遠く、また私の解釈に過ぎません。他のクラスを使って自分の描き方を追加できます。例えば、Three.jsではカメラと投影を扱う専用のクラスを使います。座標を格納するのに基本的な数学を用いましたが、もっと複雑なアプリケーションを作成したい場合や、1フレームの間にたくさんの頂点の回転が必要でも、すぐにできるわけではありません。これらを最適化するには、同次座標(射影幾何学)や四元数といった、もっと複雑な数学が必要になります。