2020年には、世界の人口は77億人になるそうだ。一方、グーグルのエリック・シュミット会長は2013年に「2020年までに地球上のすべての人がネットに接続されるだろう」と言った※1。目下、新興国でスマートフォンがものすごい勢いで伸びているのを見るとそれもありうるのかもしれない（2020年までにネット人口が半数を超えるというようなシミュレーションが多いようだが）。
遠藤諭
※1 Twitterに「For every person online, there are two who are not. By the end of the decade, everyone on Earth will be connected.」とポストした。
パイの奪い合い、ならその分け方を賢くしよう
人々は、資源でも食糧でも奪いあったり分け合っていままでやってきた（その代表は国境だろう）。このまま人口が増えていくとそうしたものが不足するのは見えているが、少しでも状況を改善するにはどうするか？ 答えは、いまよりもスマートに資源を分け合うことしかないと思う。奪いあっているのでは、エネルギーを余計使うし、安心して食糧の生産もできない。ネットにおけるシェアリングエコノミーを、はるかに大規模にしたようなしくみがあるべきだとも思う。
図1 3人でケーキを分ける例
先週、“いかにシェアすることに意味があるか？”というちょっとしたパズルをやっていた。どんな話かというと、ケーキは単純に1人ずつに切り分けていったら、相応の分けた合計の価値しかなく、切り分ける大きさに誤差があるとクレームが出ることもある。ところが、シェアリングエコノミー的にあらかじめみんなの希望を集めてからやると、なんと“ケーキは分ければ増える”というような現象が起きる。『週刊アスキー』の巻末コラムでも書いたのだが（“3人”で分けるお話）、ここでは“何人で分けても増える”ことに踏み込んでみたいと思う。
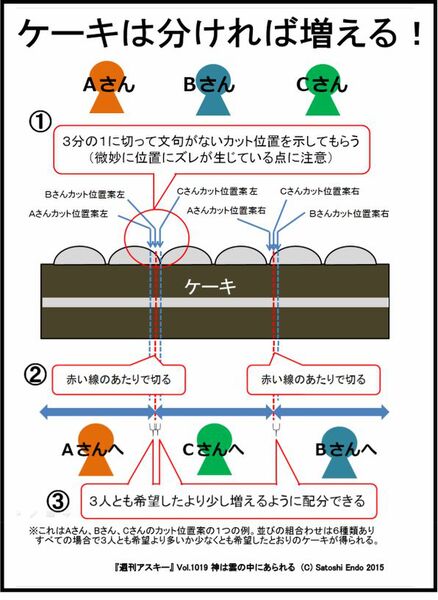
ケーキを3人で分ける場合について、整理して1枚の絵にしたのが図1である。順を追って説明すると、(1)A、B、Cの3人にどこで切ったら自分は文句を言わないか聞き、図のようなカット位置案になったとする。(2)ケーキの左から3分の1と、右側から3分の1の位置として赤い線のあたり（カット位置案の3人のズレ幅などによって正確にこの位置でなくてもよい）でケーキを切る。(3)切ったケーキをA、B、Cの3人に図のように配分する（BとCの位置が入れ替わっている点に注意）。これで、3人とも自分がカット位置案で示して得られると期待していたピースよりも大きなケーキが手に入る。
図2 みんながどんな位置順序を提案してもうまくいく（カット位置が重なったケースは省略）。
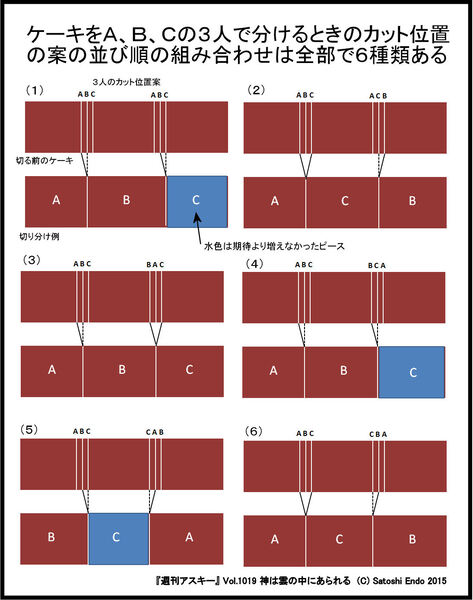
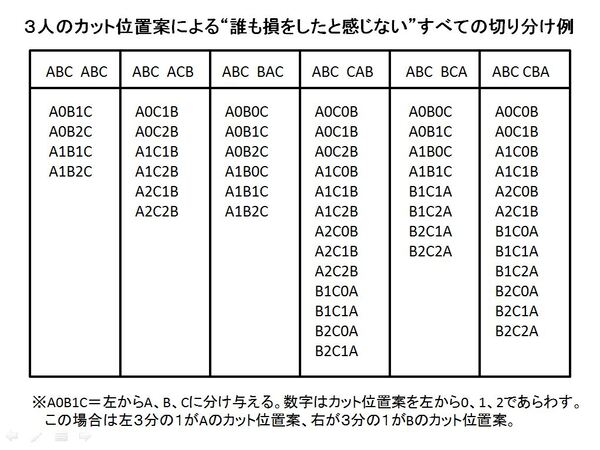
もちろん、ケーキの全体量が変化することはないのだが、3人とも自分が提案したカット位置で切ってできるピースの1つよりも少しだけ大きなケーキを得ることができる。これは、たまたまA、B、Cの3人のカット位置案がこの並び順だった場合だが、すべての並び順について示したのが図2である。これを見ると、たいていのケースで全員が自分が期待していたよりも多くのケーキが得られる（切り分け後で茶色のピース）。そして、少なくとも期待していたとおりのケーキを得ることはできる（切り分け後の水色のピース）。
実は、同じカット位置案についてケーキの分け方はいずれも複数パターンある。それは、ちょっと腕に覚えのある方なら30分もあればプログラムを書いてすべてを洗い出して検証することができる。
そのようにして求めたのが、以下の一覧である。カット位置案の6つの順列組み合わせについて、合計で49個の“ケーキが増えると感じる”切り分け方が存在する（図3）。
図3 答えとなるケーキの切り方一覧
実は、カット位置案のズレ方によってはこれ以外にも答えはあるのだが（たとえばCさんが中央のピースを取るときに左のカット位置は案より右側にきているがそれよりも大きく右のカット位置が案より右側にきていたときなど）、ここでは位置関係しかみていない。というのはズレの幅を比較できるのだとするとこの問題自体が長さを比較してやればいいでしょうとなってしまう。
関わる人の数が増えても、誰もが得をするきり分けができる
それでは、4人以上でケーキを分ける場合はどうなるのか？ 同じようにプログラムを書いてやってみると、4人の場合、5人の場合も“ケーキが増える”切り分け方があることが分かった。それなら何人で分けても“ケーキが増える”切り分け方があるのか？ 結論からいえば、何人で切り分けても“全員がケーキが増えると感じる”切り方がある。
図4 何人で分けても全員が“ケーキが増えた”と感じるケースがある。
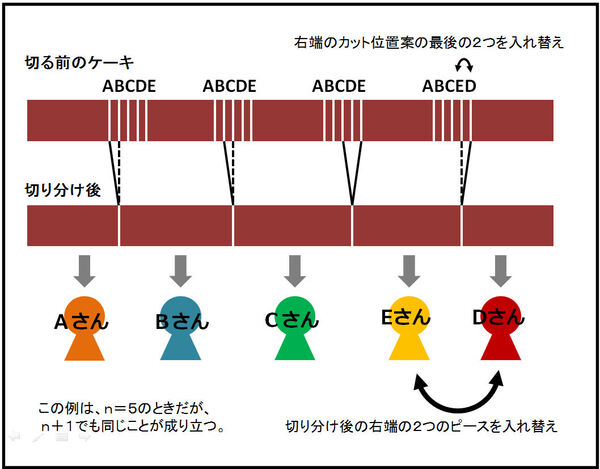
簡単に言えるのは、3～5人で分ける場合で“ケーキは増えた”わけだから、6人は3人＋3人、7人は3人＋4人、8人は3人＋5人……と見てよいからだ。あるいは、5人で分ける場合を例にとると、カット位置案が“ABCDE ABCDE ABCDE ABCED”（いちばん右端の最後の2つカット位置だけが入れ替わっている）のときに、全員が“ケーキが増えたと感じる”切り方が可能であることが示せる（図4）。同じように、n人で分けるときいちばん右端の2つのカット位置案が入れ替わっている以外のすべてのカット位置案が同じ順番になっているとき、n人全員が“ケーキは増える”となるというふうに一般化できる。
いわゆるシェアリングエコノミーを象徴するサービスとして、Uberは自動車や時間をシェアしている。Airbnbなら部屋をシェアしているし、Postmatesなら何かを届けるために自分の手間をシェアしたりしている。そこで重要なのは、誰が何を希望していて、何を提供できるか？ が分かる“場の共有”である。今回のケーキを分割する例では、みんなの希望をあらかじめ集めただけといえるが。
切る人と選ぶ人を変えれば、より公平な分配はできてはいた
実は、ケーキを3分割する方法について、今回の切り方がよい方法なのかというとまるでそうではない。まず自分は増えないのに他人が増えるケースがある（図2の水色のピースをつかむことになったケース）。次に配分の方法は複数あるからどれを採用するかも決められない可能性もある。各人の増えた分（図1で増えた分）の合計を3人で再配分すればよいという意見もありそうだが、それではふただびケーキを3人で分ける問題が発生するだけで、再帰的に問題先送りするだけだ。ちなみに、ネットを調べてみるとケーキを3人で分ける方法はいくつも提案されている。
- Aが３分の1のあたりを切る。Bが残りを2つに切る。Cが選び、Aが選び、Bが選ぶ。
- AとBで２つに分ける。AとBはそれぞれ３等分になるように分ける。Cが、AとBから1ピースずつもらう。
- Aが3等分になるように分ける。BとCが別なものを選んだときは残りをAがとる。BとCが同じものを選んだら残る２つからAが1つ取り、残りをBとCが再配分する
いずれの場合も“Aが切り、Bが先に選ぶ”という発想で公平に分けられるということを前提としている。これは、“誰が切るのか”という問題がある点でが美しくない気もする。しかし、不公平になるかどうかは、これはもう数学の中でも哲学に近い“囚人のジレマンマ”で事実を知ったあとで確率が変わるかというような問題なので安易に不公平とも言いたくない。
ちなみに(1)に似たやり方を前述のコラムで書いたがこちらの方法のほうがよさそうだ（C、B、Aの順で選ぶとすると、Bが明らかに2等分でない分け方をしたとき自分が最善の次のピースを得ることができる）。
同じ量への分配だけでなく、いつ手に入るかという価値を加わえる
しかしでは、こんなふうになかなかよい切り方が提案されているなら、今回の切り方に意味がないのかというとそうではない。シェアリングエコノミーのいまの時代には、これをネットサービスにあてはめると話が違ってくる。
ネットではたくさんの人がバラバラな時間にサービスを利用していて、他人がどうなったか見えていないケースが多い。たとえば、クラウドファンディングでは、早めにお金を入れた人は、より安い価格で対象商品を手に入れることができたりする。私は、いまKickstarterで“Pebble Time”というスマートウォッチにお金を入れているが、最初の1万人は159ドルで、次の3万人は179ドルで買える。その次の人たちは商品到着日が1ヵ月遅れるといった設定になっている。ネットの非同期性やそれによる蓄積交換的なしくみが、これを許容しているといえる。シェアリングエコノミーにおける分配は、完全に公平である必要はないということだ。
しかも、人間の価値観もバラバラで、それぞれ持てるものも違っていて、それが必要なタイミングというのも違っている。そのデコボコなピースを組み合わせることで、ハッピーの総量が100％を超える（今回のケーキの切り分け方では各人の3分の1と思う位置にズレが生じていたのがデコボコだったわけだ）。そうしたことは、いままでの世の中でもあった。お宝を山分けする場合に各人で欲しいものが違ったら、やはりハッピーの総量は増えたはずだ。しかし、それをシステムとして設計できるようになったことがシェアリングエコノミーたるゆえんである。
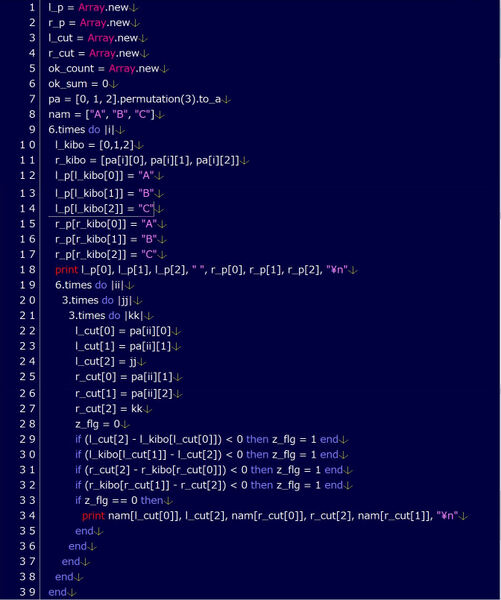
以下に、ケーキを3人で分ける切り分け方を検証するプログラムを示す。さすがに、世の中はこんなに簡単ではないわけだがとにかくシェアすることは正しい。
3人でケーキを分けるプログラム（この程度のコードでも3人のカット位置案が出てきたときにできるだけハッピーの総量が増える切り方を選べるようになる）。
P.S. 今回のケーキを分ける問題とは違うコンピュータにおける不思議な現象について書いたことがある。『近代プログラマの夕』（ホーテンス・S・エンドウ著、アスキー刊）の“ハードディスクの容量を２倍にする方法”というやつだ。これは知り合いがソフトも書いたのだが、ハードディスクの残り容量を2倍で表示するようにしておけば、自分は2倍のハードディスクを持っていることになるというお話（使うたびに2倍の速度で減っていくだけなのだが＝ハードディスクは正常な状態でもファイルの大きさ以上の容量を消費していく）。これに近いことはネットサービスでは行われているような気もするが。
