Ponanza開発者が語るディープな将棋AIの話 第3回

電王・Ponanza開発者が語る、“自転車置き場の議論”に陥った指し手生成祭り

将棋プログラム「Ponanza」の開発者、山本一成氏。写真は今年4月に開催した電王戦第1局のもの。

　こんにちは、将棋プログラム「Ponanza」の作者、山本一成です。実はこの連載は第1回目から大きなテーマがありました。それは、「今の人工知能は人間が完全には理解できないところまできている」ということです。しかし、そのままでいいのでしょうか。我々にはこの難題に立ち向かう方法はないのでしょうか。今回は科学における人間のバイアスについてお話します。

アインシュタインの誤解 問題編

 

「あなたの数学は正しいかもしれないが、あなたの物理学は忌まわしい」
――宇宙はなぜこのような宇宙なのか 人間原理と宇宙論（講談社現代新書より引用）

 

　アインシュタインが物理学者のルメートルに対して言った言葉です。ルメートルはアインシュタインが提唱した有名な相対性理論から、宇宙は定常状態ではなく膨らむか縮むかするはずだと演繹的に答えを出しました。しかし、アインシュタインはこの結論に対して、上記のような強い言葉を使って非難しました。答えは知っての通り、ルメートルが言ったとおり、宇宙は膨らむでいることが現在ではわかっております。

　世界最高峰の頭脳を持っていたであろうアインシュタインは、なぜ間違えてしまったのでしょうか。しかも、すごく奇妙に見えないでしょうか。自身が提唱した理論から演繹的に求められた結論に対し、なぜアインシュタインはそこまで否定的になったのでしょうか。

指し手生成祭りは自転車置き場の議論

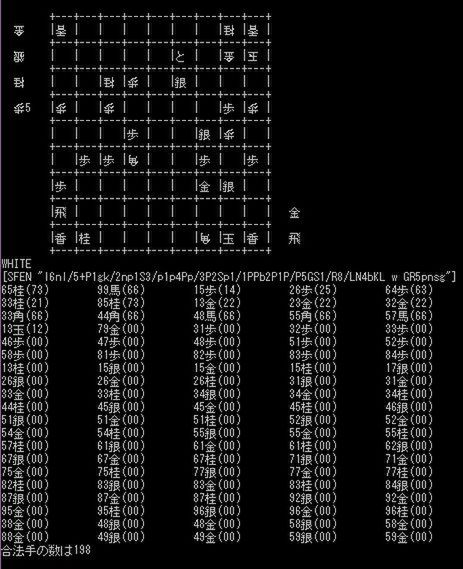
　さて、話題は変わりますが、一時期将棋プログラマーの間で指し手生成祭り(さしてせいせいまつり)なるものが流行ったことがありました。それは以下の局面の合法手（指すことが可能な手）をいかに高速で生成できるかを競うものでした。

上記は指し手生成画面。この局面における合法手は198手ですが、初期局面では30手で、局面が進むと最大で593手と言われておりますが、だいたい合法手の平均は約80手ぐらいです。

　つまり、ある局面での合法手をいかに速く高速で算出できるかを競ったのです。プログラマーにとっては当たり前とも言えますが、プログラムはうまく書けた場合とうまく書けなかった場合では、実行速度で100倍差がつくことも決して珍しくはありません。もちろん、将棋プログラムにとっても高速で動作することはすごく大切なことで、もし2倍速で動ければ、1倍速の自分自身に対して、勝率7～8割を達成できます。

　そのため、プログラマー達は必死に指し手生成を高速化していました。もちろん、指し手生成は速ければ速いほど、将棋プログラムが強くなるのは確かです。また、高速化を求めることが一概に悪いとも言えません。テンプレート特殊化やSIMD命令の駆使など、現代において高速なプログラムを組む上で必須とも言える知識をうまく勉強できるのもメリットのひとつです。
    
　しかし、将棋プログラムを強くするプログラムを書くという作業の中で、指し手生成の高速化はあくまでその一部なのです。具体的に言えば、指し手生成部分は将棋プログラム全体から見れば2％程度しか実行時間がかかっていないのです。作業に使う時間を指し手生成の高速化ばかりに割くのは、明らかにバランスを欠いています。ちょうど福笑いで、目と鼻の位置が定まっていないのに、眉毛を一生懸命整えている状態です。では、なぜこの「指し手生成祭り」が流行ったのでしょう。
    
　理由は様々あります。まず、多くの将棋プログラムが同じ土俵で計測できるということ。そして、検証にほとんど手間がかからないこと。さらに、プログラムの理屈をほぼ完全に把握できていること。最後に、少なくとも最初のうちは考えれば考えるほど良い実験結果が得られることです。要は理屈が通っており、将棋プログラムを強くする方法の中ではすごくわかりやすい手段だったのです。

　しかしながら、この指し手生成の高速化に比べて、本当に強い将棋プログラムを作るということは、非常に難しい作業になります。第1回でもお伝えしたように、すでに強い将棋プログラムを作るという作業は、人間の論理の力や直感があまり働らなかない領域にきております。つまり、理屈がわからないものに対して努力を続けることは非常に困難なので一旦保留し、理屈が完璧にわかっている“指し手生成の高速化”をひたすら頑張るという流れになったわけです。

　私はこの現象が“自転車の議論”に似ているなと思いました。発電所のような巨大で複雑なものを作る時は複雑すぎて専門家以外では議論がまったく起こりませんが、その発電所の自転車置場について議論が進んだ時は議論が紛糾することを“パーキンソンの凡俗法則”と言い、この例えの中出てくる自転車置き場の話になぞらえ、自転車置き場の議論と呼んだりします。なぜ、自転車置場といったトリビアルなことに議論が集中するのか。理由を大雑把に言ってしまえば、そこについて議論することはそこまで脳の負担ではないからです。言い変えれば、大して難しくないからです。

アインシュタインの誤解 解決編

　さて、冒頭の話に戻りましょう。なぜアインシュタインは定常宇宙にこだわり、膨らんだり縮んだりする宇宙モデルを嫌がったのでしょうか。以下は私の想像ですが、おそらくアインシュタインは辛かったのだと思います。宇宙が定常でないとすると始まりや終わりを考える必要があり、それを考えていくと当時の物理学では到底手に負えない世界が広がっていると直感したのだと思います。
    
　つまり、非定常を認めれば、すでに非常に難しい宇宙論がさらに難しいことになります。人間はつい複雑なことを無視して、簡単なことに注視しようとする性質が悪い方向に働いたのでしょう。あのアインシュタインですらそんな罠にハマってしまったのかもしれません。

見えないものを見ようとし続けることが大事

　人間は難しい問題に直面してしまった時、簡単な切り口を探しがちです。それ自体はまったく間違った行為ではないのですが、いつまでも簡単な切り口を求め続けることは必ずしも正しい判断ではないでしょう。人間はわからない状態をわからないままにしておくことにもストレスを感じ、わからないところに無理やり理由をつけようと考えるのが常です。とはいえ、この連載でも繰り返し述べているように、もはや現代の情報科学のアルゴリズムは本質的には理解できないことが普通です。しかし、理解できないことを知ってもあきらめない態度が大事なのだと思います。

　まずは理解できない自分を認め、それでもそれに向き合い続けることが、現代科学を理解して紐解く鍵となるでしょう。理解できると傲慢になるのではなく、理解できないと空虚に走るでもなく、ただ見えないものを見ようとし続けることこそが、唯一この先を見る方法になると私は信じています。

　そして、将棋プログラムを通じて、みなさまの現代情報科学の理解の一助となることができれば、私はとても嬉しいです。