石井晃（いしい・あきら） 1957年生まれ。理学博士。早稲田大学理工学部を卒業後同大で博士号取得。筑波大、ロンドン大研究員を経て鳥取大学工学研究科機械宇宙工学専攻応用数理工学講座教授に。専門は計算物理学的手法を用いた表面科学と社会物理学
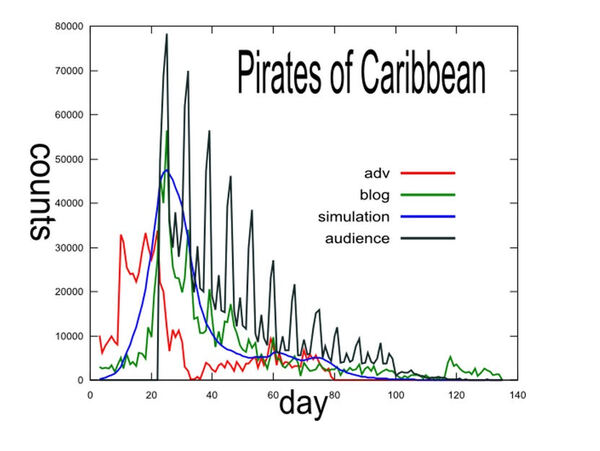
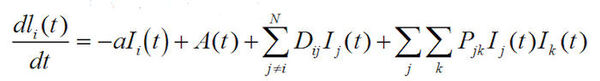消費者の感情の動きをCGMの書き込みから分析し、数理モデル化できないか――何とも野心的な内容の研究が現在進められている。研究を主導しているのは「大ヒットの方程式 ソーシャルメディアのクチコミ効果を数式化する」という著書もある鳥取大学工学部の石井 晃（いしい あきら）教授だ。数式は下記のような何とも難解なもの。しかし、ここから導き出されるグラフは、驚くほど人の動きに合致するという。もしこの公式が多くの分野で有効ならば、マーケティングの考え方が大きく変化する可能性がある。この数式はいったいどのような社会の動きを見てモデル化しているのか、お話を伺っていこう。
3つの要素を元に数式を構成した
消費者の運動方程式
「パイレーツ・オブ：カリビアン」と「スパイダーマン3」のBlog言及数と観客動員数、広告費、数式を使ったシミュレーションの4つを重ねて比較したグラフ
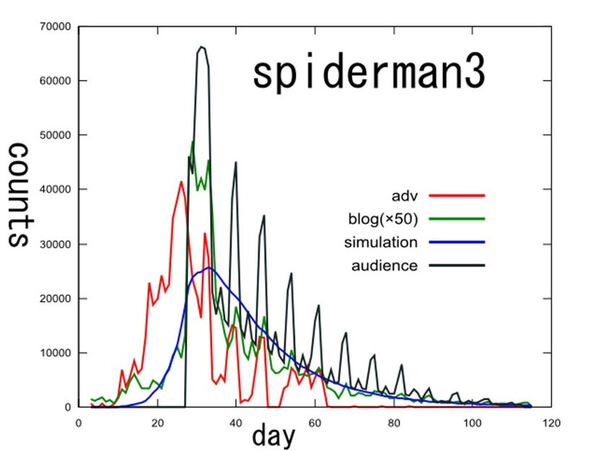
――今回「デジタルコンテンツエキスポ」で発表されていた「ヒット現象の数理モデル」ですが、関連したBlogやTwitterなどのコンテンツ数を数理モデルで分析するとヒットするものが分かるというものでした。まずもって、この長い式がどういうものかというあたりを簡単に説明していただけませんか。
はい。まず一番単純な事実として人間のうちの何パーセントは思ったことをBlogやTwitter、Facebookに書くんですよね。で、その割合がある程度決まっていれば、盛り上がればそういうネット上の書き込みも増えます。ですから本当は人々の心は計れないのですが、それの何割かの人がBlogとかTwitterに書くから、人の心の動きが近似的に分かるというものです。
――著書の「大ヒットの方程式」で、2009年9月に2695万のBlogが日本にはあって、アクティブなユーザーが328万としています。裁判員候補者名簿の通知のときに34万人通知書が送られて、通知の事実を書いてはいけないのに書いた人が0.3％もいると書かれていますよね。
| Image from Amazon.co.jp |
 |
|---|
| 大ヒットの方程式 ソーシャルメディアのクチコミ効果を数式化する |
そうです。これが多分、定量的にBlogを書いた人の数を算出した最初の例だと思います。Blogの数は計れますけど、書こうと思った人の数は分からなかったわけです。だけどあの裁判員制度の通知は34万人とはっきり分かっているわけです。なので、あれは凄くわかりやすい例となったわけですよ。
――書いてはいけないのに0.3％もいたというのが驚きでした。考えてみると、そういう人はピラミッド構造の一番頂点の人なのかなと思います。裁判員制度よりももっと身近なものだったら、もっと裾野が広がるという考え方もできるわけですか？
いや、逆に0.3％は多いですね。
――そうなんですか？
ええ。あの後、ウチの研究室の学生が映画について言及しているBlogの数を調べました。観客動員数が出ますよね。あれで映画に言及しているBlogの割合を出してみると、0.1％でした。つまり1000人に1人がBlogを書くと。裁判員制度は歴史的上初めてですし、「オレが日本の歴史の証人になる！」といった興奮が多分あって、普通より多く書いてしまったのではないかと（笑）。他のもので調べても大体0.1％というのがいいラインの数値です。
――なるほど。では数式に話を戻しますが、この数式は何を表現しているのかというあたりを詳しく教えてください。
私が考えたことを数式で表現しただけなんですが、その元の考え方はそんなに難しくありません。この式はいわゆるマーケティングで使う式と違っておもしろいのは、例えば映画のマーケティングですと広告費をこれくらい用意しました、この前の製品の実績はこれくらいでした、今度はこういう新しいプロデューサーが係わっています、この人は前にこれくらいの実績がありました、するとこれくらいが見込めます、という感じで算出していきますよね。これは逆で、売る側ではなく、買う側、つまり消費者の方程式になっているわけです。
――消費者の動きを見るわけですか。
そうです。消費者1人1人が、どういう気持ちで製品に関心を持って、その製品を買うのか、あるいは見るのかという観点で式を立てているわけです。いわば「消費者の運動方程式」になっている。具体的な項は何を言っているのかというと、3点あります。まずテレビや雑誌でやっている広告・宣伝があります。そういう露出で見て、「あ、これ買おうかな」「これを見ようかな」と消費者が思います。これがそこそこの割合があるだろうと予想したわけです。これは「広告宣伝費のそもそもの金額×ファクター」という形です。そのファクターというのは広告・宣伝のできが良ければ係数がいいし、悪ければその数値が0に近づいていきます。まずこれは直接的に影響がある。
2つ目が「直接コミュニケーション」というものです。すでに買った人、あるいは買ってはいないけれどすごく関心を持っている人が友達にその評価を言ったりしますよね。「これをオレは買いたいと思っているんだよ」「これ、凄くいいからお前も絶対に買いな」みたいなものです。いわゆる口コミです。こういう友達からの影響があると仮定して数式上ではこの友達に対して影響を「Σ」の和の記号を使って表現しています。友達は1人ではないから、友達の数だけ、例えば10人いたら、10人からそれぞれ聞いて、「すごく買いたい」と思う人もいれば、「お前の勧めるものは信じられない」という場合などを全部おしなべて計算をします。
デジタルコンテンツエキスポで公開されていた「食べるラー油」のシミュレーションと実際のBlog言及数。「間接コミュニケーション」が大きく関わると、このように爆発的な伸びを示す
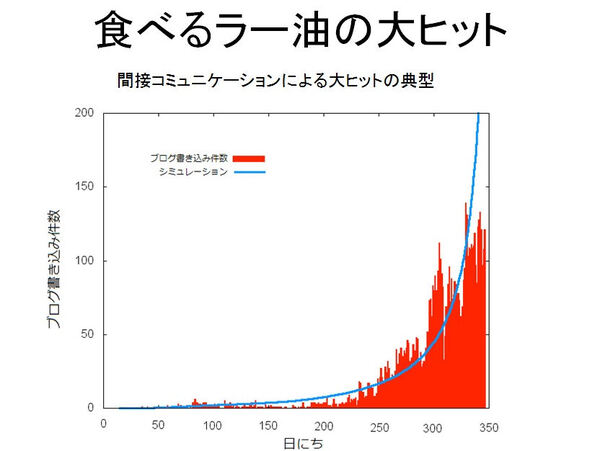
そして3つ目ですが、これがわれわれのユニークな点です。「間接コミュニケーション」といって、直接の知り合いではない者の影響を考慮しています。東京などでありがちなのが、例えば通勤通学の電車の中で、隣の女子高生がやけに熱心に話しをしていて「今日始まるドラマらしいけど、何、そんなに興奮するほどおもしろいの？」とかしゃべっている。30分揺られている間についつい話が耳に入ってしまって、結局その番組を見てしまったとかありますよね。それのポイントは、全然知り合いではないけれど、その情報が漏れてきて自分が影響を受けてしまったというものです。2002年の日韓ワールドカップを思い出してほしいのですが、第3戦が始まる前は「日本は決勝トーナメントに行けるのかな？」とどこに行っても話題になっていました。ああいう状態を想像していただくといいです。
――つまりこの数式の中には、広告費、直接コミュニケーション、間接コミュニケーションのこの3つが入っているという形ですね？
そうです。それを全体としてではなくて、1日ごとに算出したものです。1日ごとというのは、口コミを聞いて「これはいいね」と思う、あるいは思ったことをBlogに書き込みます。そのBlogに書いたことがまた別の人の影響になるわけです。要するに前日のその動きは、翌日にはそのままその人の広告に現れるので、そういう形で口コミとか間接コミュニケーションとかで盛り上がると、それが結局はまだ関心を持っていない人の関心を呼び起こすことになるということが式に入っているわけです。
