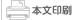Rubyで学ぶRuby 第3回

Rubyで「木」を扱う

こんにちは。Rubyを作りながらRubyを学ぼうという連載企画、第3回です。第1回と第2回では、Rubyインタプリタとは何か、Rubyでプログラムを書いて動かす方法、そして「変数」「分岐」という基本的な言語機能について学びました。

ここで、ちょっと根源的な質問について考えてみてください。 プログラミングとは、いったいなんなんでしょう？

この質問の答えは、どういう話をしているかによって、かなりいろいろなものが考えられます。 とはいえ、ものすごくざっくりとした答えとして、「プログラミングとは『何かを都合よくいじること』である」というものがありえるでしょう。 ゲームのプログラムなら、「何か」に相当するのはキャラクターとか弾とかで、その状態をプレイヤーの操作などに応じて変化させていくことでプログラミングします。 前回の記事で書いたプログラムで「何か」に相当するのは、「数」や「文字列」です。それらを単純に計算したり、分岐を使って異なる結果を得たり、反復を使って手作業では面倒なことをコンピュータにやらせたり、そういうプログラミングをしていました。

さて、この連載で最終的に作りたいプログラムは、Rubyインタプリタです。 Rubyインタプリタをプログラミングする場合の「何か」に相当するものはなんでしょうか？ 私たちが作るRubyインタプリタの仕事は、MinRubyというプログラミング言語で書かれたプログラムを実行することなので、 「MinRubyのプログラム」がいじりたい「何か」に相当しそうです。 しかし「MinRubyのプログラム」は、「数」とか「文字列」に比べるとかなり複雑なので、もっといじりやすい形にする必要があります。 そんなときに使い勝手がいい形として、「木」というものがあります。

「木」は、そこそこ複雑なものをプログラムで扱いたい場合に便利な「構造」です。 そこで今回は、この「木」をRubyで扱う方法を説明します。 具体的には、「配列」と「関数」について学びます。

木を作ったり、変形したり、ものを取り出してきたりできるようになれば、かなりの問題をプログラミングできるようになると言っても言い過ぎではないでしょう。 ここら辺からすこし話が小難しくなる部分も出てきますが、がんばってついてきてください。

配列：値をまとめる

木を説明するために、まずは複数の値をまとめて扱う方法について話をします。たとえば、10と20という2つの値をまとめるには、Rubyでは次のように書きます。

pair = [10, 20]

このように、複数の値をカンマで区切って「[」と「]」でくくれば、変数pairに「10と20をまとめたもの」が入ります。

本当に10と20が入っているのか、pairの中身をpで見てみましょう。 次のようなRubyプログラムを書いてファイルに適当な名前で保存し、ターミナルやコマンドプロンプトからrubyプログラムで実行してみてください。 （Rubyプログラムの実行方法を忘れてしまった人は第1回の記事を読み直しましょう。）

pair = [10, 20]
p(pair)

実行結果はこんなふうになるはずです（try-pair.rbという名前のファイルに上記のプログラムを保存した場合の例です）。

C:¥Ruby > ruby try-pair.rb ⏎
[10, 20]
C:¥Ruby >

変数pairの中身は、10と20がペアになったもののようですね！

pair = [10, 20]のように「[」と「]」で括って複数の値をまとめる機能のことを配列といいます。 「変数pairは、10と20という2つの値をまとめた配列である」、というわけです。

こんなふうにプログラムと実行結果を別々に書いているとスペースばかり使ってしまうので、 この先の説明では上記の流れを次のように書いて示すことにします。

pair = [10, 20]
p(pair) #=> [10,20]

つまり、プログラムの中で「#=>」に続けてその行の実行結果を示します。 Rubyプログラムでは「#」より後ろに書いたものは無視されるので、これをそのままプログラムとして実行しても支障ありません。

こんなふうにしてプログラム中にコメントとして実行結果を書き残す方法は、Rubyのリファレンスやブログ記事などでもよく使われています。

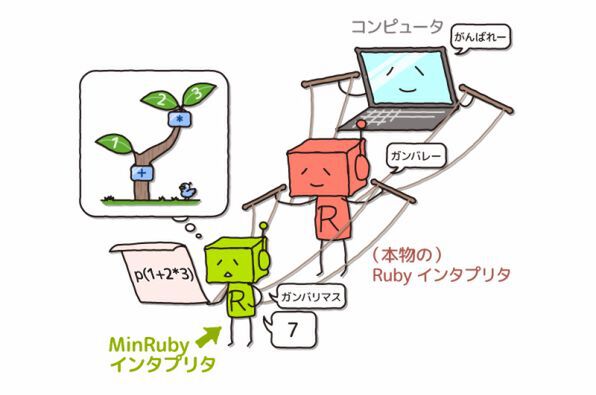
今度は、配列から値を取り出してくる方法を見てみましょう。 配列pairから1つめの値を取り出すには、pair[0]のように書きます。0は「0番目」という意味で、この配列には2つしか値がないので、左側の値のことを指します。

left = pair[0] # 0: 左の値を指す
p(left) #=> 10

同様に、右の値を取り出すには次のように書きます。

right = pair[1] # 1: 右の値を指す
p(right) #=> 20

上の例では2つの値の配列を扱いましたが、3つ以上の値でも同様に配列として扱えます。

ary = [10, 20, 30]
p(ary[0]) #=> 10
p(ary[1]) #=> 20
p(ary[2]) #=> 30

逆に、1個だけしか値がない配列も作れるし、値が0個、つまり値を持たない配列も作れます。

ary = [10]
p(ary) #=> [10]
p(ary[0]) #=> 10
ary = []
p(ary) #=> []

値とは何か

先ほどの説明では、配列は「値」をまとめると言いました。しかし、そもそも「値」とは何なのでしょうか。

プログラミング言語における値とは、「それ以上計算が進まない式」のことです。たとえば、1は値です。いっぽう、1 + 2は計算が進む余地があるので値ではありません。1 + 2を計算して3になれば、これは値です。

値は整数だけとは限りません。前回なんとなく出てきた"あたり！"というのも、「文字列」という種類の値です。 したがって、["あたり！", "はずれ！"]のように文字列の配列も作れます。

実は、配列もまた値です。というのも、[10, 20]は値をまとめただけのものなので、それ以上計算が進むことはないからです。 （ただし、配列の中身に値になっていないものがあったら、その配列は値ではありません。たとえば[10 + 20, 40]のようなものは、[30, 40]まで計算が進んで初めて値になります）。

ここまで、「数値」と「文字列」、それに「配列」という3つの種類の値が登場しました。 配列の中身は、同じ種類の値である必要はないので、たとえば「数値と文字列」の配列みたいなものも作れます。

ary = [10, "じゅう"]
p(ary[0]) #=> 10
p(ary[1]) #=> "じゅう"

さらに、配列自体も値なのだから、「数値と配列」の配列、みたいなものも作れます（少しややこしいですが）。

ary = [10, [20, 30]]

慣れないと見にくいかもしれませんが、左側には10という数値が、右側には[20, 30]という配列が入っています。

p(ary[0]) #=> 10
p(ary[1]) #=> [20, 30]

aryから20を取り出してみましょう。まず、aryの右側の値（配列）を取り出し、その値から右側の値を取り出します。

right_ary = ary[1]  # 右側の値を取り出す
p(right_ary)        #=> [20, 30]
p(right_ary[0])     #=> 20

上記の例では、わかりやすくするためにright_aryという別の変数を用意してそこにいったんaryの右側の値を入れましたが、余分な変数を介さず一気に取り出すこともできます。

p(ary[1][0]) #=> 20

ary[1]からさらに0番目を取り出したいので、ary[1]の後ろに[0]を指定しています。

さらにややこしいですが、「配列の配列」は値なので、「配列の配列の配列」を作ることもできます。 「配列の配列の配列の配列」を作ることだってできます。 実は、この「配列の配列の…の配列」という考え方が、次の節で「木」を表現するときに重要になってきます。

「木」とは

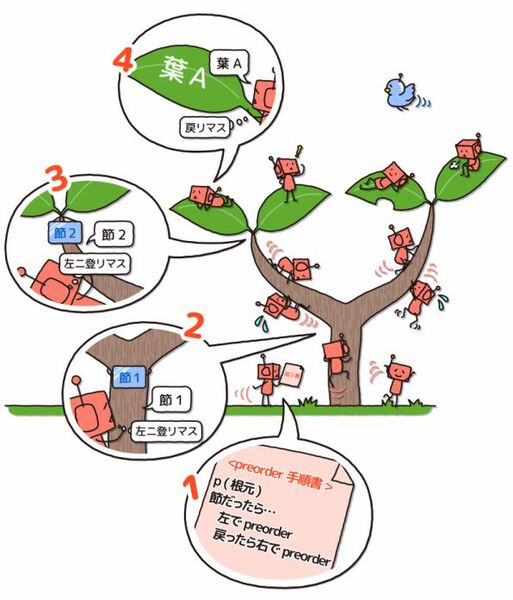
では、今回の本題に入ります。コンピュータ科学の世界における「木」とは、複数のものに親子関係を与えたものです。

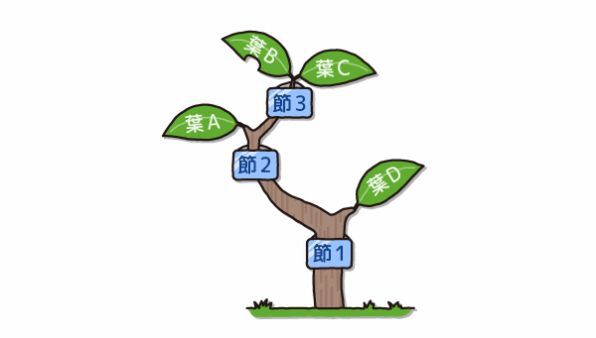
といっても、なんのことかよくわかりませんよね。たとえば、次のような植物の「木」の絵を思い描いてください。

この木の絵で、下にあるほうを「親」、上にあるほうを「子ども」と呼ぶことにします。 たとえば、一番下の(節1)は、(節2)と(節3)を子どもに持ちます。(節2)は、(葉A)と(葉B)を子どもに持ちます。同様に(節3)も、(葉C)と(葉D)を子どもに持ちます。(葉A)から(葉D)は子どもを持ちません。

木では、この例のように、親は複数の子どもを持てます。逆に、1つの子が複数の親を持つことはできません。また、誰かの親であっても、別の誰かの子である場合もあります（節2や節3がそうなっています）。 子どもを持つものを節（せつ）といい、持たないものを葉（は）といいます。この例では、その名のとおり、(節1)～(節3)が節で(葉A)～(葉D)が葉です。

どの木にも、親を持たない節がただ1つあります。そのような節を根（ね）と言います。上の例では(節1)が根です。

節や葉には好きな値をひとつ持たせることができるのですが、今回はそのまま節や葉の名前の文字列を持たせることにします。たとえば(節1)には"節1"という文字列を、(葉1)には"葉1"を持たせます。

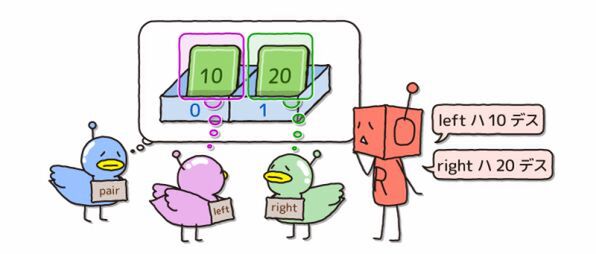
それでは、このような木をRubyプログラムで表現する方法を考えましょう。 木には親や子がいくつかあるということは、複数のものが集まっているわけだから、配列を使えば木を表現できそうです。 実際、上の絵の木をRubyプログラムで表現すると、次のように書けます。

node1 = ["節1", ["節2", ["葉A"], ["葉B"]], ["節3", ["葉C"], ["葉D"]]]

かっこだらけで何が何だかわからないですね。順を追ってこの木のつくり方を見ていきましょう。

部分的な木

一般の木について考察しましょう。

木には、「ある節とその子どもたちだけを取り出したものも木になっている」、という面白い特徴があります。たとえば、さっきの例の木で(節2)とその子どもたちだけを取り出してみます。

(節2)が根であり、その子として(葉A)と(葉B)があるだけの小さな木になっています。こういうふうに全体の木からある節とその子どもたちを取り出した木のことを「部分木」といいます。(節3)とその子どもたちを取り出しても、やはり木になります。 逆に考えると、「(節2)を根とする部分木」と「(節3)を根とする部分木」の2つを子どもに持つ節に、(節1)という名前をつけたものが、元の木だったといえます。

ここで、(節2)の木をさらに分解してみます。コンピュータ科学の世界では、葉が1つだけでも「木」と呼びます。

この「木」はただ1つの葉が根になっていて、親子関係はひとつもありません。

ここでも逆に考えると、「(葉A)を根とする木」と「(葉B)を根とする木」の2つを子どもに持つ節に、(節2)という名前をつけたものが、(節2)の部分木だった、といえます。

逆に考えてばっかりだと思うかもしれませんが、この観察が重要です。つまり節というのは、複数の部分木とその名前を「まとめたもの」であるということです。したがって、値を「まとめる」配列を使えば節が表現できるということになります。

木を構築する

では、実際にRubyの配列で木を表現していきましょう。最初に登場した木の絵を例に使います。

まず、葉1つからなる木を表現するために、「名前の文字列1つだけからなる配列」を使うことにします。

leaf_a = ["葉A"]

なぜこうするのか？ということが気になるかもしれませんが、とりあえず深く考えずに進んでください。他の葉も同様に作っておきます。

leaf_b = ["葉B"]
leaf_c = ["葉C"]
leaf_d = ["葉D"]

次に、節を表現します。例として考えている木の(節2)を表現しましょう。

すでに述べたように、節というのは、部分木（と名前）をまとめたものです。(節2)の部分木は、leaf_aとleaf_bです。また、節の名前は"節2"です。これらの値を配列としてまとめれば、節になります。

node2 = ["節2", leaf_a, leaf_b]

名前、左の部分木、右の部分木、という順番で配列に入れました。(節3)のほうも同様に表現できます。

node3 = ["節3", leaf_c, leaf_d]

最後に(節1)です。これもやはり部分木をまとめたものです。ここでいう部分木は、(節2)と(節3)になります。

node1 = ["節1", node2, node3]

これで、(節1)を表現した配列を作ることができました。ここではわかりやすさのためにnode2やleaf_aなどの中間変数を使いましたが、直接node1を定義すると次のようになります（ちょっと前にチラ見せしたものとまったく同じ形です）。

node1 = ["節1", ["節2", ["葉A"], ["葉B"]], ["節3", ["葉C"], ["葉D"]]]

見にくいので、改行とインデントを使って、もう少しわかりやすく表現してみます。 ちなみにRubyでは、こんなふうに配列の「[」と「]」の中に改行を入れてもかまわないことになっています。

node1 = [
  "節1",
  ["節2", ["葉A"], ["葉B"]],
  ["節3", ["葉C"], ["葉D"]]
]

ここで示した木の表現方法は一例であって、ただ1つの方法ではありません。 たとえばここでは「名前、左の部分木、右の部分木」という順番で配列に格納しましたが、この順番は例えば「左の部分木、右の部分木、名前」としても構いません。また、今回は節や葉の名前に文字列を使いましたが、整数を使っても構いません（ただしこの表現方法を変えると、この先で木を分解していく際のプログラムも合わせて変える必要があります）。 この連載では深入りしませんが、木の表現方法は実に様々な方法があり、それぞれにメリットとデメリットがあります。

木を分解する

配列を使って木を作ることができたので、今度は作った木を分解してみます。

根（ね）の名前を取り出すには、配列の0番目を見ればいいですね。

p(node1[0]) #=> "節1"

左側の部分木を取り出すには、1番目を見ます。

node2 = node1[1]
p(node2) #=> ["節2", ["葉A"], ["葉B"]]

右側の部分木は2番目です。

node3 = node1[2]
p(node3) #=> ["節3", ["葉C"], ["葉D"]]

取り出した部分木から名前を取り出したり、そのまた部分木を取り出したりするのも同様です。たとえば、(節2)の部分木から、名前と部分木2つを取り出してみます。

p(node2[0]) #=> "節2"
p(node2[1]) #=> ["葉A"]
p(node2[2]) #=> ["葉B"]

このように、節に対しては、0番目を取り出すとその節の名前、1番目からは左側の部分木、2番目からは右側の部分木が得られる、ということを覚えておいてください。

ちなみに、葉は名前1つだけからなる配列として表現しているので、部分木を取り出すことはできません。

leaf_a = node2[1]
p(leaf_a[0]) #=> "葉A"
p(leaf_a[1]) #=> nil
p(leaf_a[2]) #=> nil

このように、長さ1の配列に対して1番目や2番目の値を読み出そうとすると、nilになります。このnilは、Rubyで「無」を表す特殊な値です。

関数：木をあやつる強力な道具

手作業で木を作ったり分解したりする方法はわかりました。次は、もう少しプログラムっぽく木をあやつることを考えていきます。題材として書くプログラムは、「木の名前」を順番に全部出力していくプログラムです。

この例で「木の名前」といっている場合の「木」は、「木全体」のことではなく、 「木の中にある部分木」たちのことです。 つまり上記のプログラムがすることは、「ある木を受け取り、その部分木（節や葉）をすべてたどって、 そのときに部分木の名前を表示する」です。

説明は後にして、今回は最初に答えとなるプログラムを見てみましょう。

def preorder(tree)
  p(tree[0]) # 各部分木でやりたい処理
  if tree[0].start_with?("節")
    preorder(tree[1])
    preorder(tree[2])
  end
end
node1 = ["節1", ["節2", ["葉A"], ["葉B"]], ["節3", ["葉C"], ["葉D"]]] # 動作確認用のデータ
preorder(node1)

とりあえず動かしてみましょう。 上記をファイルに保存して、rubyプログラムで実行してみてください。

C:¥Ruby > ruby tree-names.rb ⏎
"節1"
"節2"
"葉A"
"葉B"
"節3"
"葉C"
"葉D"

見事、木に含まれているすべての部分木の名前（つまりすべての値）を表示することができました。

関数で木をたどる

すべての部分木をいっぺんに考えるのは無理なので、いちばん大きな木だけを考えてみましょう。 木そのものの名前、つまり根の値を表示するには、木を表す配列の先頭の値を取り出せばいいのでした。 treeという変数に木が入っているとしたら、その木の名前は次のようにして取り出せます。

p(tree[0])

いまやりたいことは、木の中のすべての部分木において、これと同じプログラムの断片を実行することです。 そうすれば、木に含まれる部分木の名前を全部列挙することができます。

木の中にある一部または全部の部分木に対して同じ処理を行うプログラムでは、 木をたどるための強力な道具として、関数というものが使えます。

関数は、プログラム断片を「使い回しできる道具」にしたものです。 さきほどのプログラム断片p(tree[0])を、関数という「使い回しできる道具」にしようというわけです。 次は、その方法を見てみましょう。

関数を定義する方法

まず、さきほどのプログラム断片p(tree[0])を、def preorder(tree)とendでくくります。

def preorder(tree)
  p(tree[0])
end

これだけで、作りたい道具にpreorderという名前をつけて定義できました。 これを関数定義といいます。 この例では道具の名前をpreorderとして関数定義しましたが、名前は好きなものをつけてかまいません。

これで関数は定義できましたが、これを書いたプログラムを保存してrubyコマンドで実行しても、画面には何も出力されません。 道具を作っただけで、道具を使っていないためです。この道具を使うには、次のように書き足します。

preorder(node1) #=> "節1" が出力される

このように道具を使うことを、関数を適用するといいます。

これでめでたく根の名前が1つ表示されました。しかし、根の名前しか出力されません。木に含まれるすべての名前を出力したいのですが、preorderは部分木をどう扱えばいいか何も知らないため、このようになるのです。

関数の中で関数を適用する

次は、preorder関数に部分木の扱い方を教えてあげる必要があります。

まず、いまの状況を整理してみましょう。

• 元のプログラム断片p(tree[0])は、ある部分木treeについて、その名前を出力するものです。
• treeの部分木であるtree[1]やtree[2]についても、同じプログラム断片を実行したいと考えています。
• そのプログラム断片は、すでにpreorderという名前の「使い回しできる道具」になっています。
• この道具を使うには、木に対してpreorder(...)と書けばよいのでした。

これらの観察を組み合わせると、部分木であるtree[1]やtree[2]についてもpreorder(...)を適用すればいいのではないか、と思い至ります。次のように書いてみましょう。

def preorder(tree)
  p(tree[0])
  preorder(tree[1])
  preorder(tree[2])
end

preorderの定義の中でpreorderの適用をしています。このように、関数定義の中で自分自身を用いることを再帰と言います。

node1にpreorderを適用して実行してみます。

preorder(node1)
 #=> "節1"
 #=> "節2"
 #=> "葉A"
 #=> NoMethodError
 #=> preorder.rb:4:in `preorder': undefined method `[]' for nil:NilClass (NoMethodError)
 #=>               from preorder.rb:5:in `preorder'
 #=>               from preorder.rb:5:in `preorder'
 #=>               from preorder.rb:5:in `preorder'
 #=>               from preorder.rb:9:in `<main>'

"節1"、"節2"、"葉A"まではいい感じに動きましたが、そこでNoMethodErrorと出力されてしまいました。 これは、Errorとあるとおり、一種のエラーです。何が起きたのでしょうか。

treeの名前だけではなく、tree全体を出力してみれば、何が起きているのかわかります。

def preorder(tree)
  p(tree)            # p(tree[0]) から一時的に変更
  preorder(tree[1])
  preorder(tree[2])
end
preorder(node1)
 #=> ["節1", ["節2", ["葉A"], ["葉B"]], ["節3", ["葉C"], ["葉D"]]]
 #=> ["節2", ["葉A"], ["葉B"]]
 #=> ["葉A"]
 #=> nil
 #=> preorder.rb:5:in `preorder': undefined method `[]' for nil:NilClass (NoMethodError)
 #=> (略)

出力の3行めに注目してください。まず(節1)の木が表示され、次に(節2)の部分木が表示され、その後(葉1)にたどり着いています。葉は部分木を持たないので、tree[1]がnil（「無」の値）になります。preorderはtreeが部分木であると仮定していますが、そこにnilという想定外の値がきたために、変なことになったのです。

ではどうすればいいかというと、部分木がちゃんと存在する場合にだけpreorderを適用すればいいのです。特定の場合にだけ実行するプログラムを書くには、第2回で登場したif文を使うのでしたね。

def preorder(tree)
  p(tree[0]) # 各部分木でやりたい処理
  if ... # 条件を埋める
   preorder(tree[1])
   preorder(tree[2])
  end
end

条件には何を書けばいいでしょうか？ 部分木がちゃんと存在する場合とは、このtreeが葉ではなく節である場合です。いま扱っている木では、葉ではなく節の場合には名前の先頭が「節」という文字になっています。そこで、名前の文字列が"節"で始まるかどうかで、treeが節かどうかを判断することにしましょう。文字列が"節"という文字列で始まるかどうかは、Rubyに備わっている.start_with?という機能を使って、.start_with?("節")とすれば確かめることができます。

def preorder(tree)
  p(tree[0])  #  各部分木でやりたい処理
  if tree[0].start_with?("節")
    preorder(tree[1])
    preorder(tree[2])
  end
end

これで、すべての名前を出力するプログラムが完成しました。

関数を使って木をあやつる話は、他にもまだまだいっぱい話すべきことがありますが、今回はここまで。

treeが節か葉かを判断する別の手段として、tree[1]を実際に読み出してみた結果がnilになるかどうかを見るという方法もあります。treeが葉の場合はtree[1]はnilになり、treeが節の場合はtree[1]は部分木になります。よって、tree[1] != nilという条件を書けばいいのです。

計算の木

今回の記事の最後に、木がなぜインタプリタの実装で重要なのかを触れておきます。その理由を一言でいえば、「プログラムというのは木で表される」ためです。

簡単な例として、1 + 2 * 3というプログラム（というか計算式）を考えます。これを木で表すと以下のようになります。

「足す」と「かける」の記号が節、整数が葉に入っています。

計算というのは、この木を葉から根に向かって処理していくことです。まず、(*)の節より上の部分木に注目します。2と3の葉がぶらさがっています。これは部分木全体で2 * 3を表現しているので、6になります。次に木全体を見ると、「1と、右の部分木の値を足す」という意味になっています。右の部分木はさきほど6になったところなので、1と6を足して7になります。1 + 2 * 3は7なので、一致しました。確かにこの木は計算を表しているようです。

インタプリタの仕事とは、この「計算の木」をたどったり操作したりして、計算を行うことなのです。

（なおこの節や葉には、名前ではなく、演算子の種別を表す文字列を持たせます。たとえば1 * 2 + 3 * 4という計算式を木にすると、(*)という値を持つ節が2つ現れることになるので、一意な名前ではなくなります。）

木の概念は、インタプリタに限らず、コンピュータの世界で至る所に現れます。 身近なところでは、ファイルやフォルダは木の一種です（フォルダが節、ファイルが葉）。 チェスや将棋の人工知能も、やっているのは木を扱うことです （盤面の状態を節とし、その節はそこから1手進めた盤面を子どもとして持つ「ゲーム木」と呼ばれる木をうまくたどって、より勝利盤面に近そうな子どもを探していく）。 他にも、データベースや経路探索など、幅広く応用されています。

まとめ

Rubyの配列を使って「木」を表現することと、関数という道具を使って「木」を分解することを駆け足で学びました。

次回は、いよいよ「計算の木」を計算するプログラムを書いていきます。簡単に言えば「電卓のプログラム」、大げさに言えば「四則演算だけからなるプログラミング言語のインタプリタ」です。お楽しみに。

練習問題

１.さまざまな木

次の木をRubyで表現してみてください。それを手作業で分解したり、preorderを適用したりしてみてください。

2. 葉だけ列挙する

preorderをいじって、葉の名前だけを出力するようにしてみてください。次のように動けば正解です。

preorder(node1)
  #=> "葉A"
  #=> "葉B"
  #=> "葉C"
  #=> "葉D"

ヒント：treeが葉である場合、すなわちtree[1]がnilである場合だけp(tree[0])を実行すればいいでしょう。

帰りがけ順

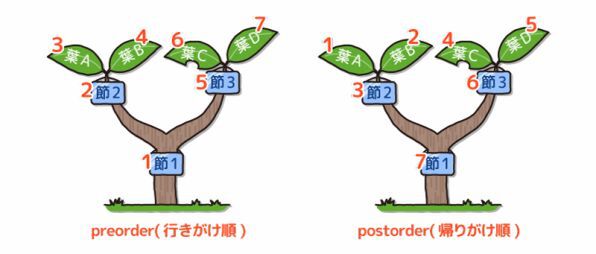
preorderは、「行きがけ順」と呼ばれる順序で名前を出力します。木を矢印でしめす順でたどり、それぞれの節や葉に最初にたどり着いたときに名前を出力するという順序です。

逆に、その節や葉に最後にたどり着いたときに名前を出力するのを「帰りがけ順」と言います。preorderを元に、帰りがけ順で名前を出力するpostorderを書いてください。次のように動けば正解です。

#=> "葉A"
#=> "葉B"
#=> "節2"
#=> "葉C"
#=> "葉D"
#=> "節3"
#=> "節1"

ヒント：今は、関数の最初にp(tree[0])を実行しているので行きがけ順になっています。帰りがけ順は、関数のどこで出力を実行すればいいでしょうか。

第2回の練習問題の答え

1. ループの間違い探し

変数iは1で初期化され、ループの先頭でi = i + 1が実行されるので、iは2になります。その後answer = answer + iが実行されるので、answerに最初に足されるのは2になります。つまりこれは、1+2+...+1000ではなく2+3+...+1001を計算していることになります。

2. 偶数だけ足し算する

answer = 0
i = 1
while i <= 1000
  if i % 2 == 0
    answer = answer + i
  end
  i = i + 1
end
p(answer)

3. FizzBuzz

i = 1
while i <= 100
  if i % 3 == 0
    if i % 5 == 0
     p("FizzBuzz")
   &else
     p("Fizz")
   end
 else
    if i % 5 == 0
     p("Buzz")
   else
     p(i)
    end
  end
  i = i + 1
end