ロードマップでわかる！当世プロセッサー事情 第185回

CPU黒歴史 大損失と貴重な教訓を生んだPentiumのバグ

　インテルのこうした動きは、当然ながら互換CPUメーカーには追い風であった。例えば、問題が露呈してすぐに「Cyrix Instead」という広告を打ったCyrixはなかなか優秀だったと思う(言うまでもなく「Intel Inside」のパロディだ)。他にも当時のNetNewsでは、「Intel Insane」(インテル狂ってる)が流行ったことを筆者も覚えている。

　その追い風がそれほど続かなかったのは、一度全量交換を決めてからの、インテルの動きが素早かったためだ。ほどなくIBMなどからの製品出荷も再開されることになった。

Pentiumで採用された割り算の方式
SRT法とは？

　そもそもPentiumのバグ問題とは何だったのか？　それは「割り算を行なう時に変な結果になる場合がある」というものだ。除算命令である「FDIV」を実行する時のみ発生したので、俗に「FDIV問題」(FDIV bug、FDIV flaw)と呼ばれている。これはPentiumの世代から、計算の高速化を狙って導入した「SRT法」に起因する。

　元々インテルでは486まで、「引き放し除算」(nonrestoring divisionとも)という方式を使っていた。例えば「987÷12」を計算する場合、人間は図1のような方法で計算する。

図1 人間が「987÷12」を計算する場合

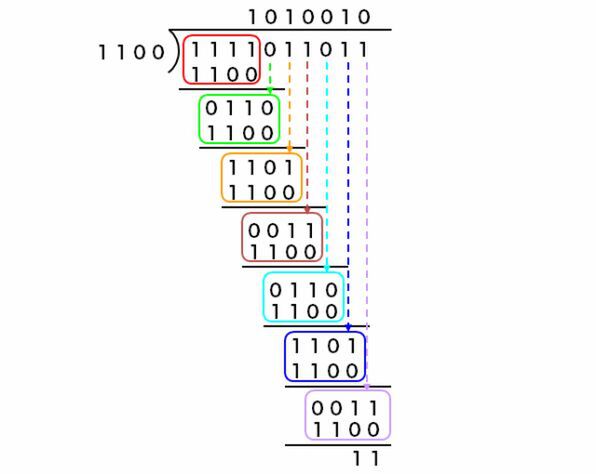
　ところがCPUの計算は、当然二進数になる。「987」は「1111011011」で、「12」は「1100」になる。そこで2進数で同じように計算すると図2のようになる。

図2 CPUが「987÷12」を計算する場合

　まず上位4桁(除数の1100が4桁だから)をマッチングすると、商が「1」と出る。ここから1bit右にシフトして、先程のあまりの「011」に次の「0」を加えて、「0110」と「1100」をマッチングし、商が0になる。そんな調子で、1bitずつシフトしながら割り算を繰り返してゆき、最終的に商が「1010010」(82)で、あまりが「11」③と計算できるわけだ。こうして「シフト演算＋減算」だけで、除算は構成できる。

　言うまでもなく、この方式は時間がかかる。なにせ1回につき1bitずつしか処理できないからだ。例えば32bit同士の演算を考えた場合、最悪なのは非除数(割られる数)が32bitで、除数(割る数)が1bitのケースだ。この場合、減算32回とシフト31回が必要になるから、合計63回の演算をしないと結果がでない。

　Pentium以降で採用されたSRT法(SRT Division)とは、一度に2bitを演算する方法である。この方式は開発者であるSweeney、Robertson、Tocherの名を取って、SRT法と呼ばれている。そもそも引き放し除算の場合、1bitずつの処理になるから、商は常に「0」か「1」である。では2bitならばどうかというと、商は0、1、2、3のいずれかになる。そこで、A÷Bを計算する場合には、以下の3つを同時に計算する。

• ①A÷B
• ②A÷2B
• ③A÷3B

　この3つの計算により、以下のように判断できる。

③の商が「1」	商は「3」
③の商が0、②の商が「1」	商は「2」
③と②商が0、①の商が「1」	商は「1」
③②①の商が「0」	商は「0」

　この方式は一見すると、手間がかかるように見える。だが、2倍は2進数の場合シフト演算1度で済むし、3倍は「1倍＋2倍」で、これも比較的容易である。何より、①～③を同時に行なえるから、回路規模こそ増えるものの時間は短縮できる。